
Gerhard Kloos*
In diesem Beitrag werden Optiken mit unterschiedlichen Objekt-, Bild- und Blendenlagen betrachtet. Zur Beschreibung der optischen Strahlengänge wird eine Matrixmethode [1,2] benutzt. Sie beruht auf einer Linearisierung der zugrundeliegenden Gleichungen für Brechung und Reflexion und ist daher auf die paraxiale Näherung beschränkt. Diese Beschreibung wird auch als Gaußoptik bezeichnet [1].
Sie eignet sich, um eine Vielzahl von Aufgabenstellungen der technischen Optik zu behandeln. Ein bekanntes Anwendungsbeispiel ist die Auslegung optischer Resonatoren in der Lasertechnik [3,4].
Im Folgenden sollen optische Anordnungen mit ausgezeichneten Objekt-, Bild- und Blendenlagen, insbesondere telezentrische Optiken, dargestellt werden. Es wird eine Einteilung (Klassifizierung) dieser Optiken hergeleitet.
1 Einführung
Um Optiken im Rahmen der Gaußoptik zu beschreiben, benötigt man bestimmte, einfache Grundelemente. Sie lassen sich wie Bausteine zu komplizierteren Anordnungen zusammensetzen. Ein besonderer Vorteil der Gaußoptik liegt darin, dass sich viele optische Systeme bereits mit einer sehr beschränkten Anzahl von Grundelementen beschreiben lassen. Wesentliche Züge der Optiken lassen sich so herausarbeiten und erkennen. Allerdings werden Feinheiten der Auslegung, die für die optische Korrektion wichtig sind (wie etwa die Asphärisierungen optisch wirksamer Flächen), in dieser Näherung nicht wiedergegeben. Eine Erweiterung eines Ansatzes mit dünnen Linsen auf eine verfeinerte Beschreibung mit dicken Linsen ist im Rahmen der Gaußoptik hingegen durchaus möglich. Ein weiterer Vorteil dieser Betrachtungsweise ist die vergleichsweise einfache und sehr übersichtliche mathematische Darstellung durch Matrizen. In diesem einführenden Abschnitt werden Matrizen für die geradlinige Ausbreitung eines Lichtstrahles, für die Brechung an einer Grenzfläche und für eine Linse vorgestellt. Für die Gaußmatrizen weiterer Bauelemente wie zum Beispiel Spiegel und Retroreflektoren sei auf die Literatur verwiesen.
Translationsmatrix
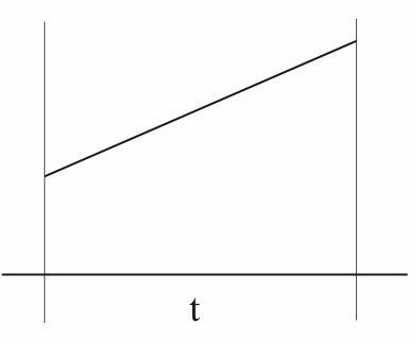
Für den Eingangs- und für den Ausgangswinkel wählen wir die Bezeichnungen \(\beta^{(1)}\) beziehungsweise \(\beta^{(2)}\). Der Abstand zur optischen Achse in der Eingangsreferenzebene wird mit \(y^{(1)}\) und der entsprechende Abstand in der Ausgangsreferenzebene wird mit \(y^{(2)}\) bezeichnet. Nach Durchlaufen des Abstandes t zwischen den beiden Ebenen ergibt sich die folgende Beziehung: ![]()
Für kleine Winkel lässt sich die trigonometrische Funktion linearisieren. Das entspricht der paraxialen Näherung:
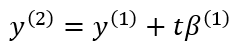
Die beiden Gleichungen für Ausgangsortskoordinate und Ausgangswinkel können in einer Matrixgleichung zusammengefasst werden: 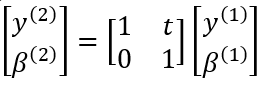
Somit erhält man für die Translationsmatrix, die die Propagation des Lichtstrahles zwischen den beiden Referenzebenen beschreibt, die einfache Form ![]()
Refraktionsmatrix
Zur Beschreibung der Brechung des Lichtstrahles an einer gekrümmten Grenzfläche zwischen zwei Medien mit unterschiedlichen Brechungsindizes wird eine weitere Gaußmatrix benötigt. Bei der Herleitung wird angenommen, dass die Form der Grenzfläche in erster Näherung durch den Radius R eines Kreises (beziehungsweise einer Kugel) beschrieben werden kann (Bild 2). Die Grenzfläche trennt optische Materialien mit den Brechungsindizes \(n_1\) und \(n_2\).
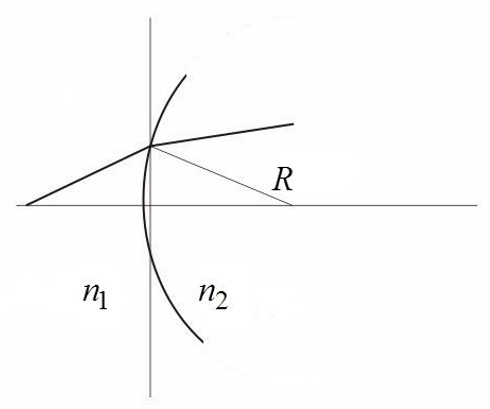
Die beiden Abstände zur optischen Achse können als gleich angenommen werden. ![]()
Für die Beziehung zwischen den Winkeln gilt eine kompliziertere Bedingung, nämlich das Brechungsgesetz. ![]()
Die beiden Winkel, die in der Gleichung auftreten, werden bezüglich der Flächennormale gemessen. Um zu einer Matrixdarstellung übergehen zu können, werden die beiden trigonometrischen Funktionen linearisiert und man erhält eine Beziehung, die in der paraxialen Näherung gültig ist. ![]()
Man stößt nun auf das Problem, dass Winkelmaße bezüglich der optischen Achse benötigt werden, um das Matrixverfahren anwenden zu können.
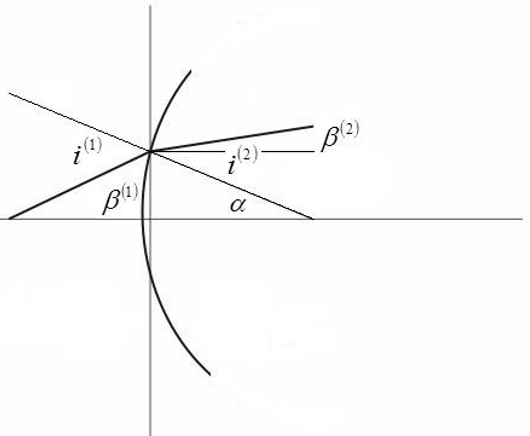
Ein Blick auf Bild 3 zeigt, dass die Beziehung zwischen den im Brechungsgesetz auftretenden Winkeln und den für das Matrixverfahren benötigten Winkeln durch den Außenwinkelsatz hergestellt werden kann: ![]() ,
,![]()
Nun kann man die drei Gleichungen zusammenfügen.
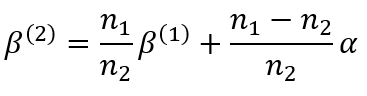
Hierin „stört” zunächst das Auftreten des Winkels alpha, da er nicht in den gesuchten Formalismus von Eingangs- und Ausgangsrelationen passt. In der paraxialen Näherung lässt sich jedoch der kleine Abstand zwischen dem Schnittpunkt der Grenzfläche mit der optischen Achse und der Bezugsebene vernachlässigen. Dann kann dieser Winkel näherungsweise wie folgt angeben werden:
![]()
Erneutes Linearisieren der auftretenden trigonometrischen Funktion ![]() führt zu einer Gleichung mit der gewünschten Struktur.
führt zu einer Gleichung mit der gewünschten Struktur.
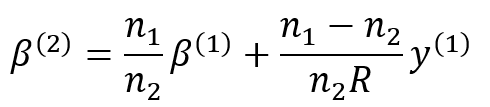
Nun lässt sich eine Beziehung zwischen Eingangs- und Ausgangsgrößen aufschreiben.
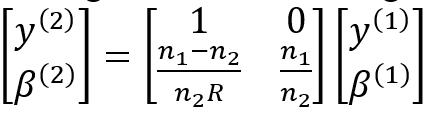
Der Zusammenhang zwischen diesen Größen wird durch eine Gaußmatrix vermittelt.
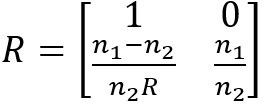
Sie beschreibt die Brechung an einer Grenzfläche.
Linse
Eine Linse lässt sich durch das Zusammenfügen der Grundelemente beschreiben. Dies geschieht durch Matrizenmultiplikation.
![]()
Damit wird die Abfolge brechende Eingangsfläche, Propagation durch die Linse und brechende Ausgangsfläche beschrieben. Ausführlicher hat diese Matrixkette die folgende Form:
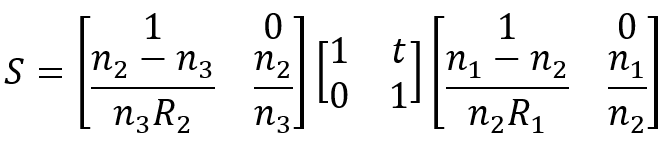
Darin sind R_1 und R_2 die Radien der beiden die Linse begrenzenden Flächen und t bezeichnet ihre Dicke. Für eine Linse in Luft gilt \(n_1=1, n_2=n\) und \(n_3=1\). Somit finden wir für die Linse die Matrix
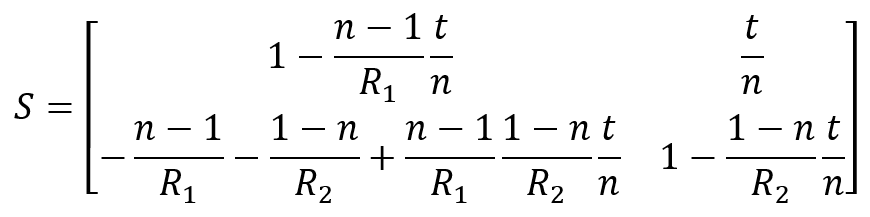
Die beiden Größen, die das Maß der Brechung an der jeweiligen Fläche beschreiben, werden nun mit einem Symbol notiert, ![]() und
und ![]() .
.
Dies führt zu einer etwas übersichtlicheren Schreibweise für die Einträge der Matrix.
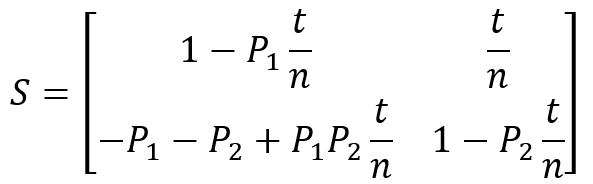
Die beschreibende Matrix einer sogenannten „dünnen Linse“ erhält man, wenn man die Linsendicke in dieser Matrix gegen Null gehen lässt: ![]()
Weitere Abkürzung für die darin auftretende Brennweite ergibt: 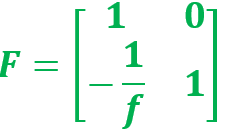
Bestimmung der Systemmatrix
Ein besonderer Vorteil der Gaußoptik liegt darin, dass die Gaußmatrix durch den Verlauf zweier geeigneter Strahlen vollständig bestimmt ist. Die Bestimmung der Gaußmatrix auf diese Weise ist analog zur Angabe der Übertragungsfunktion einer elektronischen Schaltung, wenn das Eingangs- und das Ausgangssignal bekannt sind. Betrachten wir also die Situation, dass ein bestimmter Strahlverlauf durch die technische Aufgabenstellung vorgeben ist und die Systemmatrix angegeben werden soll, die diesen Strahlverlauf bewirkt. Eingangs- und Ausgangskoordinaten der Strahlen seien für zwei Strahlenpaare a und b bekannt ![]() .
.
Es ist wichtig, dass die beiden Eingangsvektoren linear unabhängig sind. Dann kann die Systemmatrix bestimmt werden. Die gesuchte Matrix muss die beiden folgenden Gleichungen simultan erfüllen ![]() .
.
Diese beiden Gleichungen können zu einer Gleichung für die unbekannten Matrixelemente \(a_[ij]\) zusammengefasst werden.
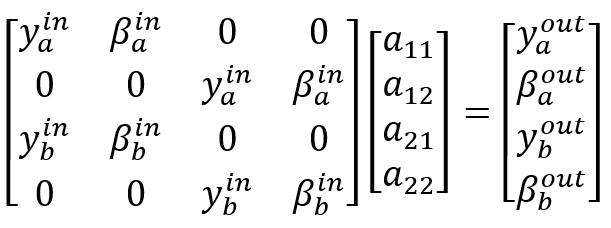
Dieses große Gleichungssystem lässt sich nun in zwei Teilsysteme aufteilen, die entkoppelt sind. Die Matrixeinträge der ersten Zeile folgen aus dem ersten Teilsystem und die Einträge der zweiten Zeile der Systemmatrix ergeben sich aus dem zweiten Teilsystem. ![]()
Zur Lösung beider Teilsysteme ist die Determinante det H nützlich: ![]()
Da die beiden Eingangsvektoren als linear unabhängig voneinander angenommen wurden, ist sie ungleich Null. Die vier Matrixeinträge der Systemmatrix lassen sich nun angeben:
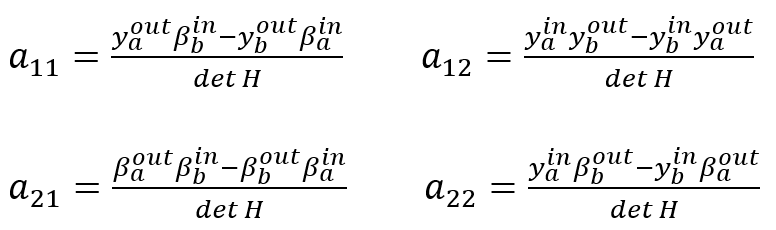
Die gesuchte Systemmatrix ist somit aufgrund der Eingangs- und Ausgangsdaten der beiden Strahlverläufe vollständig bestimmt. Als ausgezeichnete Lichtstrahlen, um eine gegebene Optik zu charakterisieren, bieten sich Hauptstrahl und Randstrahl an. Der Hauptstrahl geht vom äußersten Feldpunkt des Objektes aus und durchsetzt die Aperturblende auf der optischen Achse. Der Randstrahl geht vom Feldpunkt auf der optischen Achse aus und durchläuft die Aperturblende an ihrem äußersten Rand.
2 Deutung der Matrixeinträge
Die Betrachtung der Matrixelemente erlaubt eine Einteilung nach ausgezeichneten Sonderfällen, die jeweils Grundanordnungen der technischen Optik entsprechen. Ausgangspunkt ist die allgemeine Gleichung für die Gaußmatrix, die die Beziehung zwischen Eingangs- und Ausgangsgrößen vermittelt:
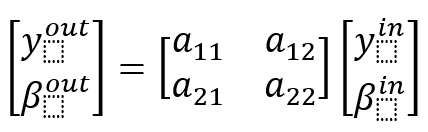
In dieser Matrixgleichung kann man die Setzung \(a_{11}=0\) vornehmen. Dann ergibt sich eine Gleichung für die Ausgangsortskoordinate, die unabhängig von der Eingangsortskoordinate ist und die nur vom Eingangswinkel abhängt: ![]()
Optisch entspricht das einer Anordnung, in der Strahlen mit demselben Eingangswinkel in einem Punkt vereinigt werden. Wir können sie daher als fokussierende Anordnung bezeichnen. Alternativ kann diese Anordnung auch als eine Optik aufgefasst werden, die aus dem Unendlichen kommende Strahlen in einem Punkt vereinigt.
Mit der Wahl \(a_{12}=0\) nimmt man eine Entkopplung der Ausgangsortskoordinate vom Eingangswinkel vor: ![]()
Das ist kennzeichnend für ein optisches System, das eine Abbildung zwischen zwei Punkten verwirklicht (Punkt-zu-Punkt-Abbildung).
Setzen wir nun alternativ \(a_{21}=0\) in der Systemmatrix, so bewirkt das, dass der Ausgangswinkel nach Passieren der optischen Anordnung nicht mehr von der Eingangsortskoordinate abhängt. Ein solcher Zusammenhang ist typisch für eine Baugruppe in optischen Teleskopen. Dieser Matrixeintrag hängt eng mit der Brennweite der Optik zusammen und Systeme, bei denen er gleich 0 ist, werden als afokal bezeichnet.
Bedeutung in der Praxis hat auch eine Anordnung mit einer Systemmatrix, deren letztes Element auf der Hauptdiagonalen verschwindet: \(a_{22}=0\). Es handelt sich dabei um eine Anordnung mit Kollimationswirkung, da nun der Ausgangswinkel nur von der Eingangsortskoordinate aber nicht mehr vom Eingangswinkel abhängt.
Zusammenfassend können diese Einzelfälle matrixartig angeordnet werden:

Das gezeigte Schema kann als eine Art Leitmotiv bei Streifzügen durch die Gaußoptik dienen. Mit den darin aufgeführten Gaußmatrizen mit verschwindenden Matrixeinträgen lassen sich keineswegs alle Gaußmatrizen erfassen, jedoch handelt es sich um vier Spezialfälle, die von besonderer Bedeutung in der technischen Optik sind. In vielen Fällen lassen sich kompliziertere Anordnungen als Verkettungen dieser Grundmatrizen auffassen und so leichter deuten und verstehen.
Nichtverschwindende Matrixeinträge können als Abweichungen von diesen ausgezeichneten Fällen gedeutet werden, zum Beispiel als Abweichung von der Bedingung für ein afokales System, Abweichung von der Kollimationsbedingung usf.
3 Aperturblende, Eintritts- und Austrittspupille
Die Aperturblende bestimmt die Bildhelligkeit und das Auflösungsvermögen einer Optik. Sie kann daher sowohl als ein Maß für die Energieübertragung durch die betrachtete Optik als auch als ein Maß für die Informationsübertragung durch diese Optik aufgefasst werden. Die Apertur- oder Öffnungsblende begrenzt den Durchmesser beziehungsweise den Öffnungswinkel des vom axialen Gegenstandpunkt ausgehenden Strahlenbündels.
Die Eintrittspupille legt den objektseitigen Akzeptanzkegel der Optik fest. Sie ist das Bild der Aperturblende wie es von einem Objekt durch die Linse gesehen wird. Die Austrittspupille bestimmt den bildseitigen Akzeptanzkegel der Optik.
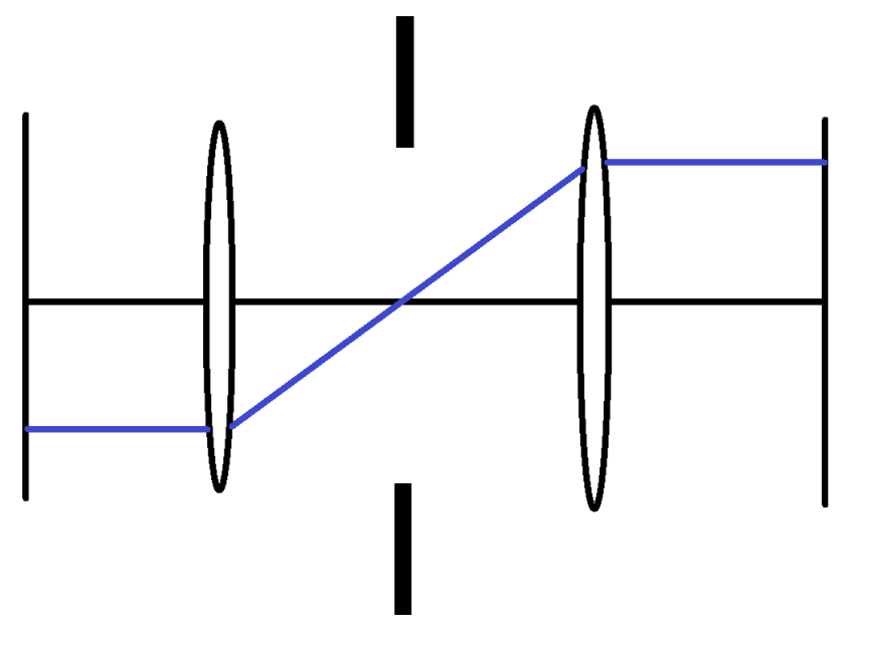
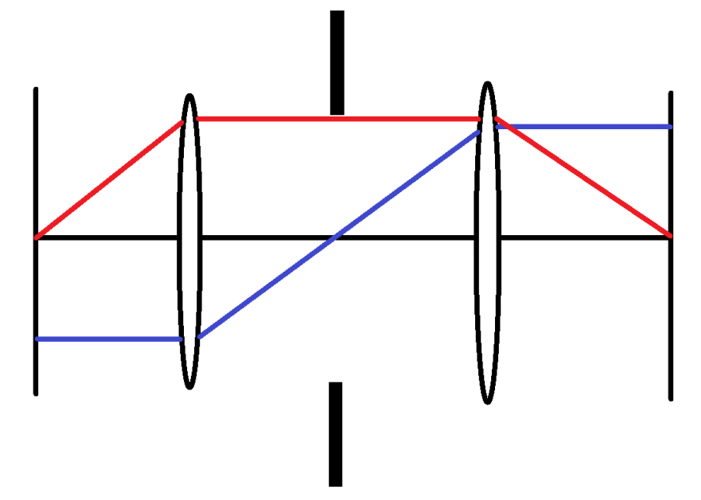
Bild 4 zeigt schematisch zwei rotationssymmetrische Linsen, die auf der optischen Achse angeordnet sind. Zwischen den beiden Linsen ist die Aperturblende angebracht. Sie legt Lage und Durchmesser der Eintrittspupille (EP) sowie der Austrittspupille (AP) fest.
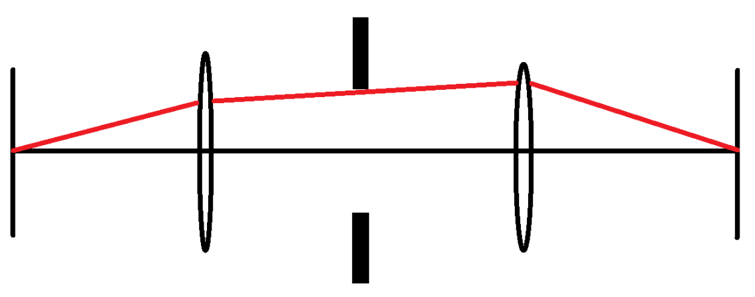
Betrachten wir zunächst die Eintrittspupille. Der Hauptstrahl ist dadurch gekennzeichnet, dass er die optische Achse in der Ebene der Aperturblende schneidet. Setzt man den Teil des Hauptstrahles, der Objekt und objektseitige Linse verbindet, gerade fort, so gibt der Schnittpunkt dieses verlängerten Strahles mit der optischen Achse die Lage der Eintrittspupille an. Um nun den Durchmesser der Eintrittspupille zu finden, verlängert man den Teil des Randstrahles zwischen Objekt und objektseitiger Linse. Der Schnittpunkt dieser Geraden mit der Ebene, die senkrecht zur optischen Achse liegt und die sich an der über den Hauptstrahl bestimmenden Position auf der optischen Achse befindet, legt den Durchmesser fest. (Der halbe Durchmesser der Eintrittspupille entspricht dem Abstand des Punktes von der Achse.)
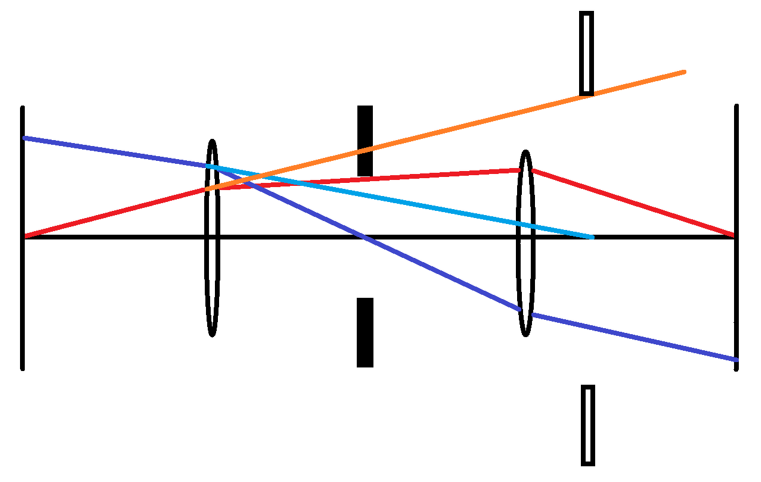
Die Konstruktion für die Austrittspupille erfolgt analog: Es wird der Teil des Hauptstrahles, der Bild und bildseitige Linse verbindet, entgegen der Lichtausbreitungsrichtung verlängert und der Schnittpunkt mit der optischen Achse bestimmt. So findet man die Position der Austrittspupille. Ihr Durchmesser lässt sich durch Verlängern desjenigen Teiles des Randstrahles, der sich zwischen Bild und bildseitiger Linse befindet, angeben. Er wird als Abstand dieser Gerade von dem zuvor bestimmten Schnittpunkt in derjenigen Bezugsebene abgelesen, die den Schnittpunkt enthält.
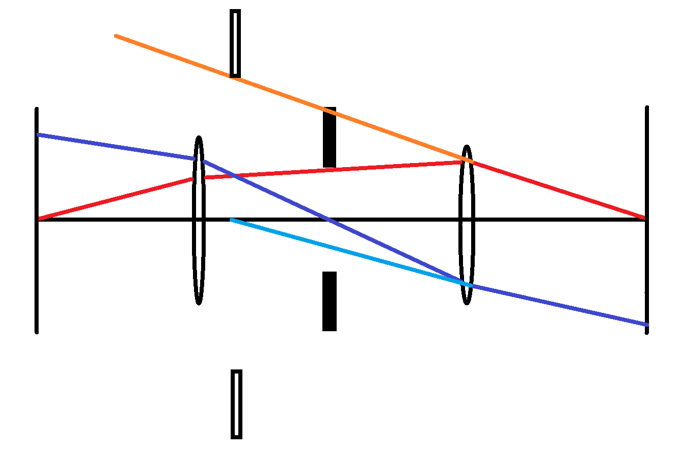
Entsprechend lassen sich Eintritts- beziehungsweise Austrittspupille für Einzellinsen angeben.
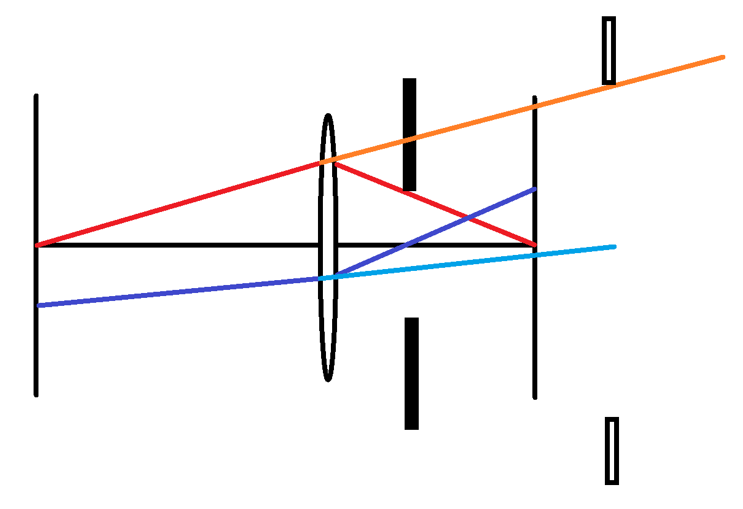
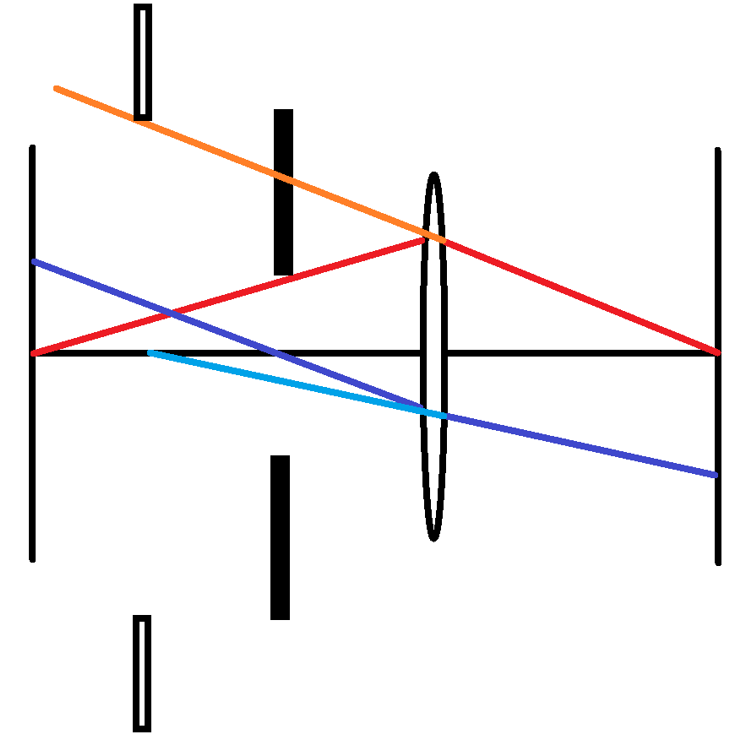
4 Telezentrische Strahlengänge
Als telezentrisch wird die Situation bezeichnet, wenn „die Pupille im Unendlichen liegt“ und der Hauptstrahl parallel zur optischen Achse verläuft.Bei objektseitiger Telezentrie liegt die Eintrittspupille im Unendlichen und der objektseitige Hauptstrahl verläuft parallel zur optischen Achse. Dies entspricht der Situation, dass der Haupstrahlverlauf senkrecht zur Objektebene ist.
Bei bildseitiger Telezentrie liegt die Austrittspupille im Unendlichen und der bildseitige Hauptstrahl verläuft parallel zur optischen Achse. Dies entspricht der Situation, dass der Haupstrahlverlauf senkrecht zur Bildebene ist.
Objektseitige Telezentrie
Objektseitige Telezentrie läßt sich durch Einbringen der Aperturblende in der bildseitigen Brennebene verwirklichen. Bild 9 zeigt dies am Beispiel einer einzelnen Linse.
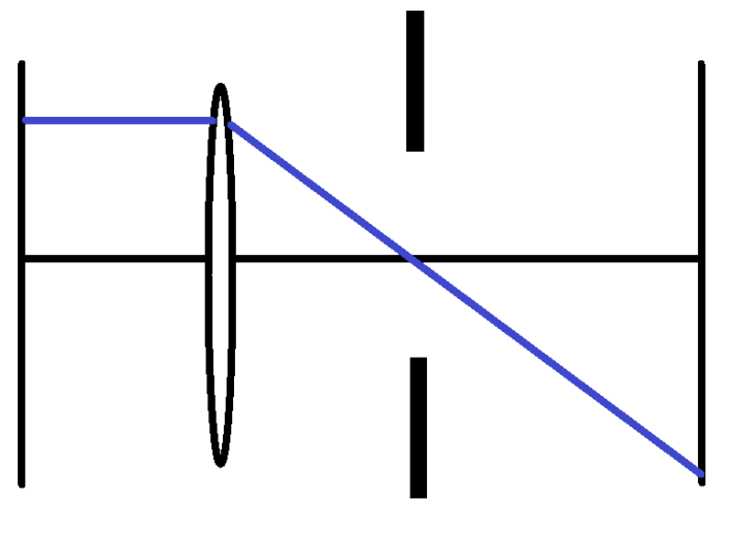
Die Strahlausbreitung bis zur Blende lässt sich durch die folgende Matrixkette beschreiben:
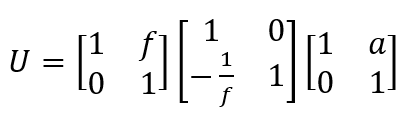
Hierin wurde der Abstand von der Gegenstandsebene bis zur Linse mit a bezeichnet und f ist die Brennweite der Linse. Die Multiplikation der drei Faktoren ergibt
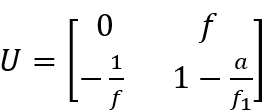
Bezeichnen wir den Abstand zwischen Blende und Bildebene mit t, so lautet die Systemmatrix für diese einfache Anordnung
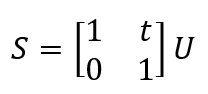
Also ergibt sich die Matrix
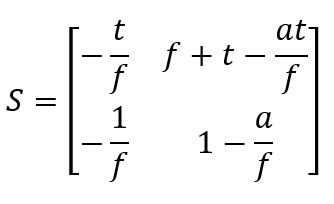
Betrachten wir nun eine abbildende Linse (Bild 10).
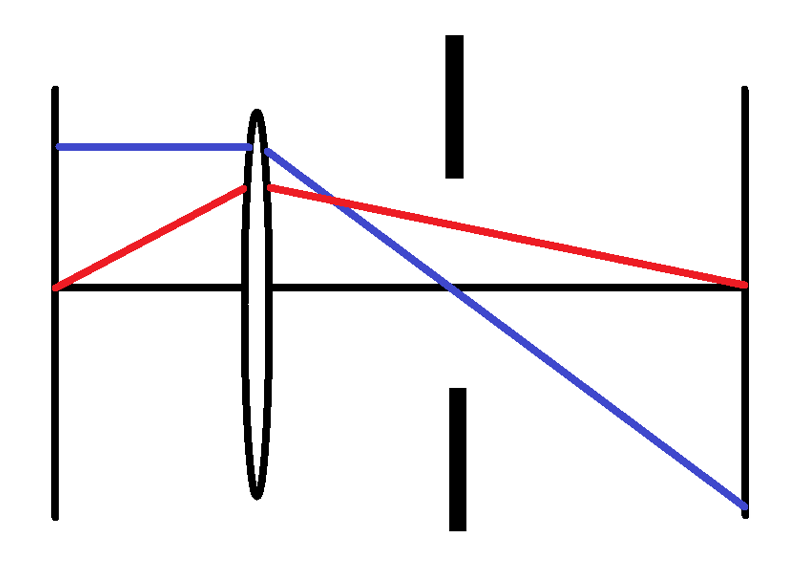
Die Systemmatrix für eine Punkt-zu-Punkt-Abbildung hat die Form:
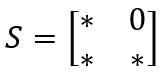
Gleichsetzen der rechten oberen Matrixeinträge führt auf die folgende Beziehung zwischen der Brennweite der Linse und den beiden Abständen:
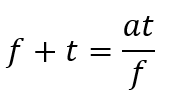
Für den Fall objektseitiger Telezentrie und einer Punkt-zu-Punkt-Abbildung ergibt sich also die Systemmatrix
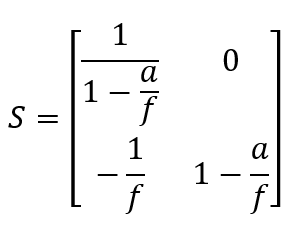
Bildseitige Telezentrie
Um bildseitige Telezentrie zu erreichen, kann die Aperturblende in der objektseitigen Brennebene positioniert werden. Bild 11 gibt eine einfache Situation wieder.
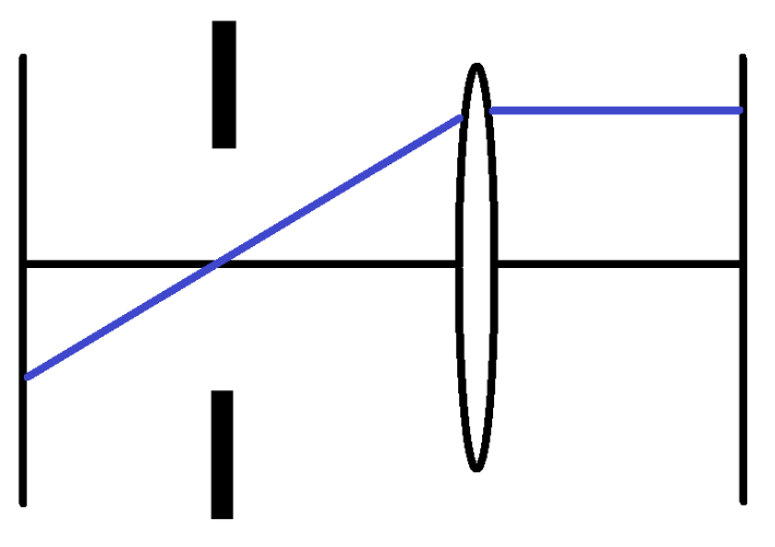
Diese Situation lässt sich durch ein Matrixprodukt mit vier Faktoren darstellen:
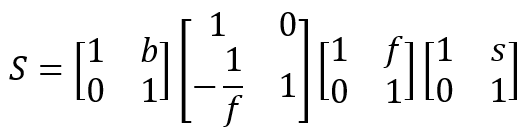
Der Abstand zwischen der Linse und der Blende wurde hier mit dem Symbol s abgekürzt und für den Abstand zwischen Linse und Bildebene wurde die Bezeichnung b verwendet. Ausmultiplizieren der Faktoren führt auf
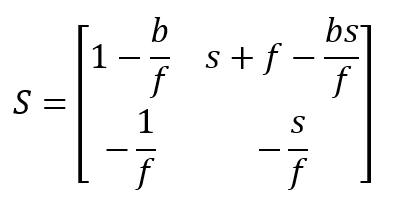
Möchte man die Situation für eine abbildende, telezentrische Linse betrachten, so führt der Vergleich mit der Matrix für eine Punkt-zu-Punkt-Abbildung auf die Bedingung:
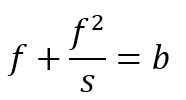
Für die Systemmatrix, die die Situation mit bildseitiger Symmetrie und einer Punkt-zu-Punkt-Abbildung beschreibt, erhält man somit
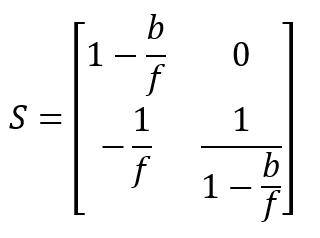
Die beiden Anordnungen aus Bild 9 und Bild 11 lassen sich auf zweierlei Arten zu neuen Optiken kombinieren: (i) man fügt sie in den Blendenebenen zusammen, (ii) man lässt die Bildebene der einen Anordnung mit der Objektebene der anderen Anordnung zusammenfallen.
Doppelseitige Telezentrie
Bild 12 zeigt die Möglichkeit (i).
Die Systemmatrix ergibt sich aus einer Abfolge von sechs Matrizen:
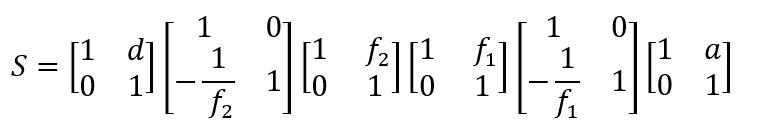
Es ist instruktiv, diese zunächst zu zwei Teilmatrizen zusammenzufassen, die den Teiloptiken vor und hinter der Blendenebene entsprechen.
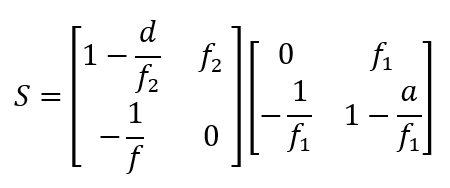
Die Systemmatrix lautet:
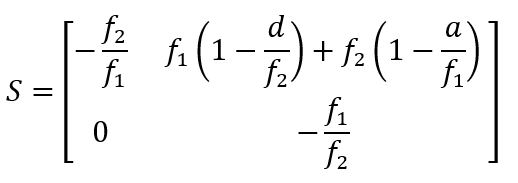
Aus ihrem rechten, oberen Matrixeintrag kann man unmittelbar ablesen, dass sich eine abbildende Optik – im Sinne einer Punkt-zu-Punkt-Abbildung – ergibt, wenn man die Linsen wie folgt positioniert:
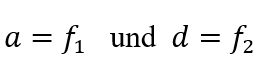
Mit dieser Setzung vereinfacht sich die Systemmatrix sehr.
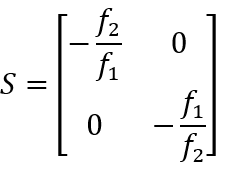
Diese doppelttelezentrische Anordnung ist hier mit Hilfe dünner Linsen dargestellt worden, um das Wesentliche zu zeigen. In der technischen Optik entsprechen den Einzellinsen häufig optische Baugruppen, die sich aus mehreren Linsen zusammensetzen.
Messanordnung
Ein Zusammenfügen entsprechend Möglichkeit (ii) kann als Ansatz genutzt werden, wenn sich das zu beobachtende Objekt in der Zwischenebene befindet. Man denke hier zum Beispiel an einen Partikelstrom, der mit einer LED-Anordnung beleuchtet und mittels einer CCD-Kamera aufgenommen wird, oder an eine Abfolge von Bauteilen auf einem Förderband.
Die Systemmatrix der optischen Anordnung folgt aus der Verknüpfung von acht Matrizen:
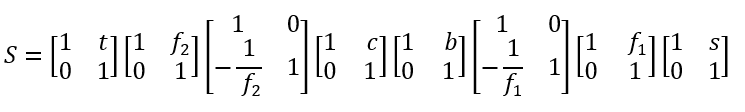
Drei davon lassen sich jeweils zu Teilmatrizen zusammenfassen, die den als dünne Linsen dargestellten Teilbaugruppen vor und hinter der Zwischenebene mit dem beobachteten Objekt entsprechen.
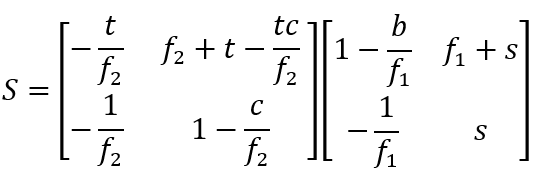
Insgesamt ergibt sich so:
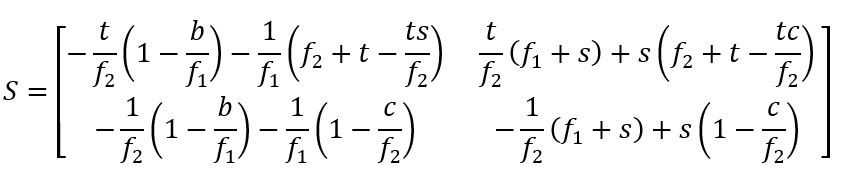
Hier ist nun der Vergleich mit einer teleskopartigen Anordnung interessant. Deren Systemmatrix hat die Form
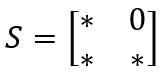
Ein Vergleich mit dem unteren linken Eintrag der Matrix für die zweistufige Anordnung führt unmittelbar auf die Bedingungen
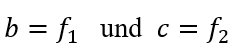
für die beiden darin vorkommenden Abstände. Die Systemmatrix nimmt in diesem Falle eine einfachere Gestalt an.
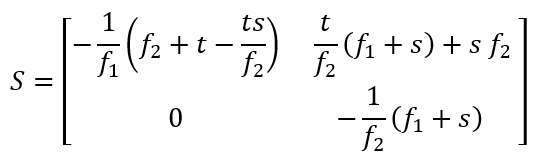
Eine solche Anordnung wird in der englischsprachigen Fachliteratur gelegentlich als Dual-Telecentric Collimator bezeichnet und damit wird zum Beispiel eine Optik angesprochen, die sich aus einer Beleuchtungseinheit und einer Objektivbaugruppe zusammensetzt. Eine solche Bezeichnung passt nicht gut zu der hier verwendeten Benennung. Ich vermute, dass ihr die Vorstellung zugrunde liegt, dass man zwei telezentrische Kollimatoren hat, wovon man den einen so dreht, dass er in Strahlausbreitungsrichtung rückwärts weist.
5 Klassifizierung
Optische Anordnungen mit Objekt- beziehungsweise Bildlagen im Unendlichen sind dadurch ausgezeichnet, dass sie Optiken mit einer bestimmten Funktion beziehungsweise mit besonderer technischer Bedeutung entsprechen. Beispiele dafür sind Optiken, die eine Punkt-zu-Punkt-Abbildung leisten, Teleskopoptiken und Kollimatoren. Ebenso haben Optiken große technische Bedeutung, die einen telezentrischen Strahlengang verwirklichen. In diesen Fällen liegen Eintritts- und/oder Austrittspupille im Unendlichen. Im Folgenden soll versucht werden, diese Vielzahl an technischen Möglichkeiten zu ordnen. Ziel ist es eine Art Landkarte zu erhalten, die einen Überblick über den Reichtum an technischen Lösungsansätzen bietet.
Zu diesem Zwecke werden die verschiedenen Kombinationen mit Lagen im Unendlichen zunächst aufgezählt (Tabelle 1). Die Reihenfolge bei dieser Aufzählung ist willkürlich.
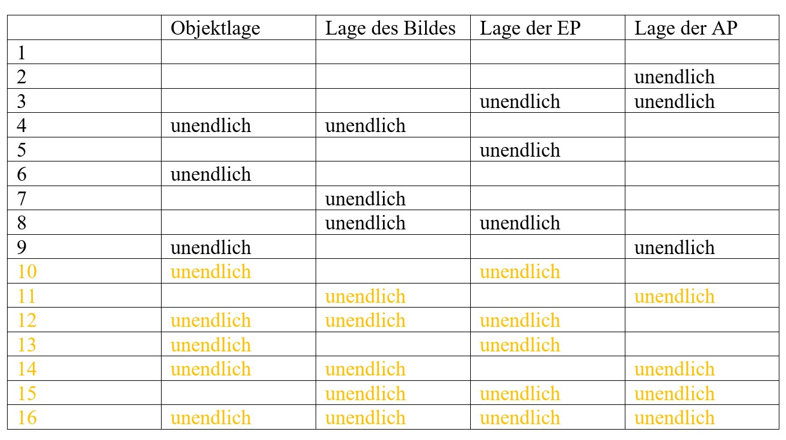
In dieser Aufzählung sind auch Fälle enthalten, die physikalisch nicht zu realisieren sind. Es gilt, dass nicht sowohl das Objekt als auch die Austrittspupille im Unendlichen liegen können. Damit entfallen vier der aufgeführten Fälle. Ebenso ist die dazu duale Aussage gültig, dass nicht sowohl das Bild als auch die Eintrittspupille im Unendlichen liegen können. Aufgrund dieser Aussage müssen drei weitere Fälle aus der Liste gestrichen werden.
Es bleiben 9 Möglichkeiten übrig. Damit sind alle optischen Anordnungen aufgezählt, die sich durch Gegenstands- oder Bildlage im Unendlichen und/oder Blendenlagen im Unendlichen auszeichnen.
In Bild 15 werden die 9 Fälle im Zusammenhang dargestellt. Als Ordnungsmerkmale dienen die Lage von Objekt und Bild sowie die Lage von Eintrittspupille und Austrittspupille. Es wird dabei von dem finiten Fall ausgegangen, das heißt von der Situation, dass sowohl Objekt- und Bildlage als auch die Lagen von Eintritts- und Austrittspupille endlich sind.
Die optischen Anordnungen werden durch eine sie charakterisierende Matrix, eine Kurzbezeichnung, die sich aus dieser Matrix und der Blendenlage ergibt, und Angaben, ob die Objekt- beziehungsweise Bildlage sowie die Lage der Eintrittspupille (EP) beziehungsweise der Austrittspupillle (AP) finit oder im Unendlichen gelegen ist, gekennzeichnet (Bild 14).

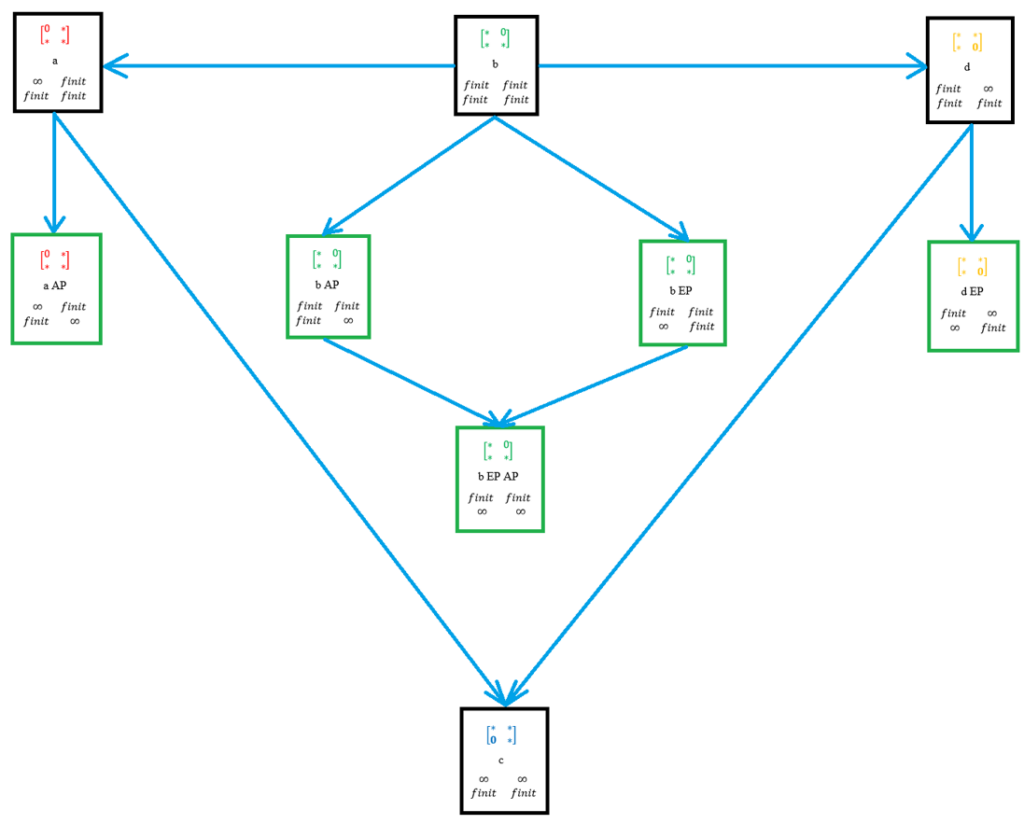
Die beiden waagerechten Pfeile bezeichnen den Grenzübergang zu Gegenstands- beziehungsweise Bildlagen „im Unendlichen“. Das gilt auch für die Pfeile, die ganz nach unten weisen. Die übrigen Pfeile kennzeichnen den Übergang zu Anordnungen mit Eintritts- und/oder Austrittspupille „im Unendlichen“. Sie weisen daher auf telezentrische Optiken.
Die Fälle (a) und (d) sind im Hinblick auf die Objekt- und Bildlage zueinander dual. Für die optischen Anordnungen (bAP) und (bEP) gilt dies bezüglich der Lage von Eintritts- und Austrittspupille. Und die mit (aAP) und (dEP) bezeichneten optischen Anordnungen sind bezüglich beider Systemeigneschaften dual zueinander.
Die optischen Anordnungen mit symmetrischen Objekt- und Bild- beziehungsweise Blendenlagen befinden sich in der Mitte der Übersicht. Symmetrisch ist hier nicht in dem Sinne gemeint, dass beispielsweise Objekt- und Bildabstand gleich seien, sondern vielmehr, dass die jeweiligen Bedingungen simultan erfüllt werden. So befinden sich zum Beispiel im Fall (b) sowohl der Gegenstand als auch das Bild in einem endlichen Abstand. Bei der Anordnung (c) ist es so, dass sie im Unendlichen liegen. Die mit (bEPAP) abgekürzte hochsymmetrische Konfiguration ist eine optische Anordnung, die bei vielen technischen und wissenschaftlichen Aufgaben Anwendung findet.
6 Beispiele
Bild 15 bietet eine Übersicht über einen Teil der „Optiklandschaft“ und eine Vielzahl von Optiken lässt sich hier einordnen.
So entsprechen viele Fotoobjektive [5,6] und die Objektive von Filmkameras der mit (a) bezeichneten Kategorie. Prominente Vertreter von Optiken mit einem Gegenstand im Unendlichen und bildseitiger Telezentrie (aAP) sind Messobjektive.
Die Bilder 16 und 17 zeigen eine Linsenbaugruppe ([5] S. 283-286) mit bildseitiger Telezentrie, die ein Objekt aus dem Unendlichen in die Bildebene abbildet.
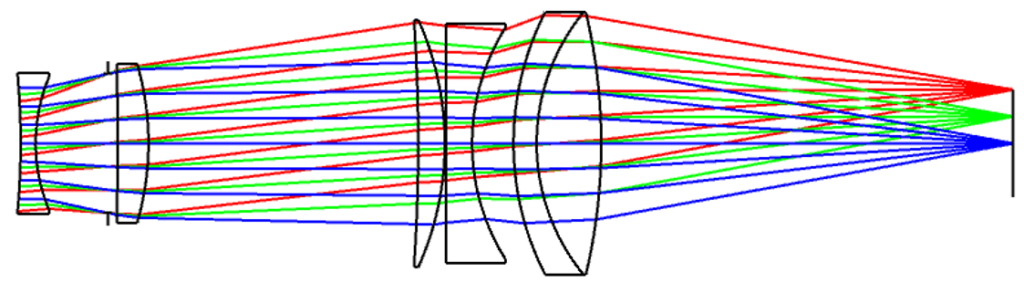
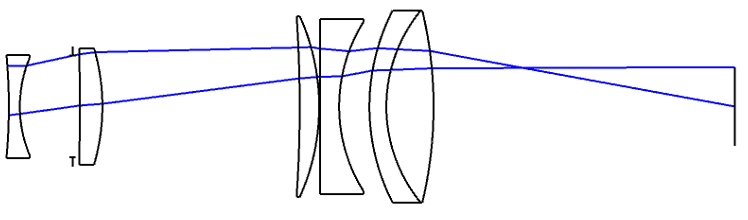
In Bild 16 sieht man drei Strahlenfächer um zur Bildebene lotrechte Lichtstrahlen. Diese Lichtstrahlen schneiden die optische Achse in der Ebene der Aperturblende. Die Anordnung (b) entspricht der klassischen Punkt-zu-Punkt-Abbildung mit finiten Objekt- und Bildlagen. Dies findet sich zum Beispiel in der Funktion von Relaylinsen [7] wieder. Auch Anordnungen zur Einkopplung der Strahlung einer Lichtquelle in eine optische Faser lassen sich so darstellen. Wird auf einen Bildsensor abgebildet, so bietet eine bildseitig telezentrische Anordnung (bAP) den Vorteil, dass die Bilderfassung toleranzunempfindlicher gegenüber Schwankungen der Sensorposition ist.
Abbildende Optiken mit einer Eintrittspupillle im Unendlichen (bEP) sind in Messobjektiven anzutreffen. Sie haben den Vorteil, dass leichte Variationen des Abstandes zwischen Messobjekt und Objektiv das Ergebnis unbeeinflusst lassen. Abbildende Optiken mit objektseitiger Telezentrie finden sich auch in den Objektiven von Mikroskopen [8]. Das Objekt kann so mit konstanter Vergrößerung beobachtet werden auch wenn es sich nicht exakt in der Brennebene befindet. Messobjektive sowie Kameraobjektive mit objektseitiger Telezentrie bieten den Vorteil, dass der Parallaxenfehler weitgehend aufgehoben wird.
Eine abbildende Optik mit beidseitiger Telezentrie (bEPAP) findet zum Beispiel bei Projektionsobjektiven für die Mikrolithographie Anwendung. Diese Objektive bilden eine mit energiereicher Strahlung beleuchtete Maske auf ein Substrat ab. Doppelseitige Telezentrie bewirkt eine gewisse Unempfindlichkeit der Anordnung gegenüber Positionsschwankungen der abzubildenden Maske beziehungsweise des Substrates, auf das abgebildet wird.
Eine solche Konfiguration (bEPAP) bietet sich auch an, um transparente Messobjekte zu durchstrahlen. Als Beispiel sei die Messung eines Beugungsgitters genannt, das sich ausbilden kann, wenn in einem transparenten Material Ultraschallwellen erzeugt werden [9]. Die Ausbreitungsrichtung der Schallwellen, die durch einen Quarzkristall erzeugt werden können, ist senkrecht zur Ausbreitung des Lichtes. Das Beugungsmuster wird durch die zweite Linse beziehungsweise Linsenanordnung auf einen Schirm oder Sensor projiziert und weiter verarbeitet.
Von besonderer Bedeutung in der technischen Optik ist die sogenannte 4f-Anordnung [10-11]. Sie folgt mit der Setzung \(f_1=f_2\) in der Gleichung für eine Optik mit beidseitiger Telezentrie und es ergibt sich eine sehr einfache Systemmatrix.
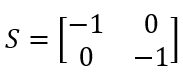
Die Vorzeichen in dieser Matrix zeigen an, dass der ausgehende Strahl in die entgegengesetzte Richtung bezüglich der optischen Achse weist und dass das Bild auf dem Kopf steht. Wie die entsprechende Anordnung mit unterschiedlichen Brennweiten weist sie in dem unteren, linken Matrixeintrag eine Null auf. Das macht die Bezeichnung „afocal relay telescope“, die sich in der englischsprachigen Fachliteratur für ein solches optisches System findet [12], sofort verständlich.
Ein wesentliches Merkmal der 4f-Anordnung ist, dass man in der Pupillenebene eingreifen und dass Ortsfrequenzspektrum formen kann. Die beiden Linsen lassen sich als „Fouriertransformatoren“ [13] auffassen. Ein besonders einfacher Fall ist das sogenannte Raumfilter, das in der Lasertechnik benutzt wird, um einen Laserstrahl zu „bereinigen“ [14]. Idealisiert entspricht es einer sehr kleinen Aussparung (pinhole) auf der optischen Achse in der Blendenebene (Fourierebene). Die Lichtstrahlen, die nun die zweite Linse verlassen, sind kollimiert und parallel zur optischen Achse. Versetzt man diese Aussparung nun in Gedanken in vertikaler Richtung so sind die Strahlen, die die zweite Linse verlassen, im paraxialen Bereich weiterhin kollimiert, aber sie verlaufen nun in einem Winkel ungleich 0 zur optischen Achse, der sich aus der Brennweite der zweiten Linse ergibt. Mit dieser Vorstellung lassen sich auch kompliziertere Vorgänge der Ortsfrequenzfilterung (spatial filtering) nachvollziehen und verstehen. In der Matrixdarstellung kann man diesen Zusammenhang wie folgt notieren:

Die Konfiguration (d), bei der das Bild im Unendlichen liegt, ist typisch für ein Okular [5]. Und sie ist kennzeichnend für einen Kollimator. Kollimatoren haben vielfältige Anwendungen und sind sowohl in der Lasertechnik als auch in LED-Optiken im Gebrauch. In der LED-Technik dienen sie beispielsweise dazu, dass von der Halbleiterlichtquelle abgestrahlte Licht in einen eng begrenzten Winkelbereich zu richten.
Eine Optik, die einen Gegenstand auf eine finite Bildlage abbildet und deren Eintrittspupille im Unendlichen liegt (dEP) ist in einigen Objektiven für Mikroskope verwirklicht. Auch in Messgeräten für die automatisierte Bildverarbeitung ist diese Eigenschaft realisiert, da die Bilderfassung auf diese Weise unempfindlicher bezüglich Schwankungen der Sensorposition ist. Insbesondere bleibt die Vergrößerung in einem weiten Bereich trotz Lageabweichungen konstant. Eine typische Messaufgabe kann beispielsweise darin bestehen, Bauteile, die über ein Förderband an der Messeinrichtung vorbeigeführt werden, zu erfassen. Dabei kann sowohl die Lateralposition der Teile variieren als auch das Förderband leichte Vibrationen zeigen. Dann ist es von Vorteil, wenn eine objektseitig telezentrische Optik eine robuste Bilderfassung sicherstellt.
Die mit (c) bezeichneten Optiken lassen sich als afokale Anordnungen [15-16] ansprechen. Hierunter fallen zum Beispiel die optischen Teleskope. Ein klassischer Vertretet ist das Galilei-Teleskop. Es zeichnet sich dadurch aus, dass der Linsenabstand der Summe der Brennweiten gleich ist.
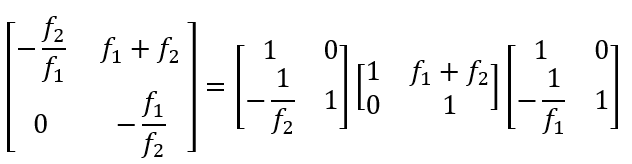
Beim Keplerschen Fernrohr entspricht der Abstand zwischen beiden Linsen der Differenz ihrer Brennweiten und die zweite Linse ist eine Zerstreuungslinse.
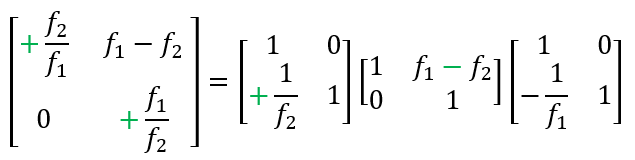
Die vorgenommene Einteilung erfasst viele bekannte Optikanordnungen. Sie kann einerseits zur Klassifizierung dienen sowie andererseits Orientierung bei der Ansatzfindung für neue Optiken bieten. Ansätze im Rahmen der Gaußoptik lassen sich unmittelbar ablesen. Die Grundfunktion des betrachteten optischen Systems spiegelt sich in seiner Matrixdarstellung wider. So lassen sich Verwandtschaften beziehungsweise Symmetrien erkennen.
Literatur
[1] S. Guillemin, S. Sternberg: Symplectic Techniques in Physics, Cambridge University Press 1984
[2] G. Kloos: Matrix Methods for Optical Layout, SPIE Press 2007
[3] A.E. Siegman: Lasers, University Science Books 1986
[4] N. Hodgson, H. Weber: Optical Resonators: Fundamentals, Advanced Concepts and Applications, Springer-Verlag 1997
[5] M. Laikin: Lens Design, CRC Press 2007
[6] S.F. Ray: Scientific Photography and Applied Imaging, Focal Press 1999
[7] G. Smith, D.A. Atchison: The eye and visual optical instruments, Cambridge University Press 1997, Kapitel 19 Relay Systems
[8] T.S. Tkaczyk: Field Guide to Microscopy, SPIE Press 2010, S. 36
[9] M. Born, E. Wolf: Principles of Optics – Electromagnetic theory of propagation, interference and diffraction of light, Pergamon Press 1980, S.595
[10] F.T.S. Yu, I.C. Khoo: Principles of Optical Engineering, John Wiley & Sons 1990, Kapitel 9.2 Coherent optical signal processing
[11] J.W. Goodman: Analog optical signal and image processing. In: M. Bass: handbook of Optics volume I: Fundamentals, Techniques, and Design, McGraw-Hill 1995, Kapitel 30
[12] J. Bentley, C. Olson: Field Guide to Lens Design, SPIE Press 2012, S. 58
[13] P. Das: Lasers and Optical Engineering, Springer-Verlag 1990. Kapitel 4.4.4 Fourier Optics and Spatial Filtering
[14] P. Heiß: Holographie-Fibel – Hologramme verstehen und selbermachen, R. Wittig Fachbuchverlag 1987
[15] W.B. Wetherell: Afocal Lenses. In: R.R. Shannon, J.C. Wyant: Applied Optics and Optical Engineering, volume X, Academic Press 1987. Kapitel 3
[16] A. König, H. Köhler: Die Fernrohre und Entfernungsmesser, Springer-Verlag 1959
* Dr. Gerhard Kloos, D-40667 Meerbusch
Titelbild: Image by Ralf Vetterle from Pixabay