
Engelbert Hofbauer, Ronald Kometer*
Teil II – erste industrielle Anwendungen
Kurzfassung / Abstract
Vignettierung heißt „Abschattung“ und bedeutet, dass Objektpunkte bzw. Objektbereiche nicht mehr oder nicht mit voller Helligkeit abgebildet werden. Bei der neuen Methode des ‚Vignettierenden Feldblenden-Verfahrens‘ wird die Vignettierung als ein physikalisches Messprinzip zur präzisen Winkel- und Positionsmessung genutzt. Im ersten Teil wurde das Prinzip und der aktuelle Stand der Technik des Verfahrens und des entsprechenden Mess-Sensors zur zweidimensionalen Messung von Winkeln und Winkeländerungen dargestellt. Dabei wurde das Verfahren zunächst rein geometrisch-optisch betrachtet und anschließend lichttechnische Effekte wie Leuchtdichte und Abstrahlcharakteristik (LVK) auf das Linearitätsverhalten beschrieben. Auf Basis dieser Grundlagen wurden theoretische Untersuchungen zu Messbereich, Linearität und der physikalischen Auflösung bzw. ‚Resolving Power‘ gezeigt. Diese wurden mit Messungen verglichen und die Abweichungen wurden diskutiert.
Im zweiten Teil werden nun bereits realisierte industrielle Anwendungen in der Fertigungsmesstechnik Optik und dem Maschinenbau vorgestellt. Dazu zählt die Winkelmessung, Ebenheitsmessung, Keilwinkelmessung und die Ebenheits- und Formmessung an großen Spiegelsubstraten. Auch die Abtragsratenmessung an einer In-Situ-Messvorrichtung mit dem DaOS-Prinzip auf einer Hebelpoliermaschine NLP 500 der Fa. Stock-Konstruktion wird näher betrachtet. Zur Asphärenvermessung kleinerer krummer Flächen mit Untersuchung von Oberflächenformabweichungen auf langwellige und mittelfrequente Fehler (MSFE) kann ebenfalls die Deflektometrische Methode mit V-SPOT-Methode angewendet und gezeigt werden.
Keywords:
Autokollimation, Großwinkelmessung, Vignetting Field Stop, VFS-Prozedur, V-SPOT, Resolving Power, Geradheitsmessung, Fluchtmessung, Fertigungsmesstechnik Optik, Deflektometrie, Asphärenmessung, MSFE, Deflektometrie, Freiformflächen
1 Einleitung Teil II: Industrielle Messtechnik mit Vignettierung
In der industriellen Messtechnik ist die klassische Autokollimation zur Messung von Klein- und Kleinstwinkeln wie z. B. zur Untersuchung der Geradheit und Ebenheit von technischen Oberflächen [1], der Messung von Führungsabweichungen von Schlitten (Kippwinkelmessung) [2] sowie in der Bestimmung der Flächenform hochpräziser optischer Flächen [3,4] nicht mehr wegzudenken. Vermehrt treten jedoch insbesondere im Automobilbau auch Anwendungsfälle auf, bei denen größere Messbereiche (±2° bis ±5°) bei größeren Arbeitsabständen (0,15 bis 2,5 Meter) gefordert werden [5,6]. Der nachfolgende Artikel soll bereits im Einsatz befindliche Anwendungen des Vignettierenden Feldblendenverfahrens in der Industrie vorstellen und beschreiben sowie Genauigkeiten und Grenzen aufzeigen.
2 Technische Anwendungen in der Praxis
Aufgrund der Ergebnisse aus dem experimentellen Teil im Vergleich zur Simulation lässt sich eine verlässliche Voraussage von Messbereich, Linearität und Auflösungsgrenze für mögliche Szenarien treffen.
Dabei sind verschiedene Anwendungen bei unterschiedlichen Konstellationen von verfügbaren Hardwarekomponenten mit unterschiedlichen Beleuchtungsanordnungen möglich und denkbar. Die Lichtquelle kann dabei sowohl spektral, im Leuchtdichteverlauf sowie in der Abstrahlcharakteristik variieren. Im Folgenden werden einige Anwendungen für das neue Vignettierende Feldblendenverfahren angegeben, welche in der Praxis bereits eingesetzt werden. Bild 1 zeigt verfügbare Applikationen und Messprozesse in der Software ELWISOFT 2.0.

Im Einzelnen sind dies von links oben nach rechts unten:
- Winkelmessung rein visuell über Monitor
- Winkelmessung mit BV-Auswertung mit hoher Auflösung
- 6 DoF Messung inkl. Fluchtungsmessung (Höhenmethode)
- Geradheitsmessung nach der Neigungsmethode
Erweiterbar zur Formmessung an Substraten nach DaOS
- 6 DoF Messung mit zusätzlichem Abstandslaser
- Prismen- und Keilwinkelmessung auch an großen Keilen
- 4 DoF Messung an optischen Geräten – Justage von Spiegeln in Lage und Winkel
- Zentriermesstechnik einseitig
- Zentriermesstechnik für Asphären
- Zentriermesstechnik beidseitig
- Brennweitenmessung
- Linearitätsmessung zur Kalibrierung-Überprüfung an AKF‘s
Die vier fett gedruckten Applikationen sowie die deflektometrische Formmessung an kleinen, stark gekrümmten Asphären werden im folgenden Abschnitt näher erläutert.
3 Geradheitsmessung nach der Neigungsmethode für lange Strecken
Die Abstandsunabhängigkeit der Winkelmessung und der Winkelempfindlichkeit gilt für unser neues Messprinzip ebenso wie beim Autokollimator mit Fadenkreuz oder mit ähnlich feststehender Objektmarke. Den Vorteil des großen Messbereiches auch auf großen Messstrecken und großen Messentfernungen bei trotzdem hoher Auflösung und Reproduzierbarkeit prädestiniert das neue Messprinzip für die Vermessung von großen Maschinen- und Fertigungsanlagen. Bild 2 zeigt eine Anwendung in der Praxis, in der ein 32 m Maschinenbett eingerichtet wird.

Die ursprünglich mit Laser-Tracker vorausgerichteten Wangen weisen zu Beginn des Justageprozesses Abweichungen in Höhe und Seite von bis zu +/- 1 mm auf (Bild 3 oben). Über einen einfachen Montage- und Justageprozess werden nacheinander die 4 schweren Granitblöcke an den Stößen bündig und in der Ausrichtung parallel gerichtet. Über seitlich angebrachte Zug- und Druckschrauben sowie Fixatoren am Fundament werden die schweren Granitblöcke mikrometerweise und auf 1/100 mm genau geschoben und bewegt, bis am Ende das Ergebnis (Bild 3 unten) anliegt. Die schwarze Kurve zeigt die Abweichung in der horizontalen Ebene, die blaue Kurve zeigt die Abweichung in der Vertikalen. In der horizontalen X-Richtung liegt die Restabweichung nach Justage und Fixierung der Linearführungen innerhalb ca. +/- 40 µm. In der Vertikalen sind die Abweichungen mit -80 µm etwas größer, kann aber im Bedarfsfall mit Hilfe einer elektronischen Wasserwaage an den Fixatoren noch nachgerichtet werden. Dies ist sowieso erforderlich, solange das Fundament noch nicht endgültig ausgetrocknet ist und sich auch die Lastverteilung der vier 40 t schweren Granitblöcke noch nicht in der endgültigen „Ruhelage“ ist.
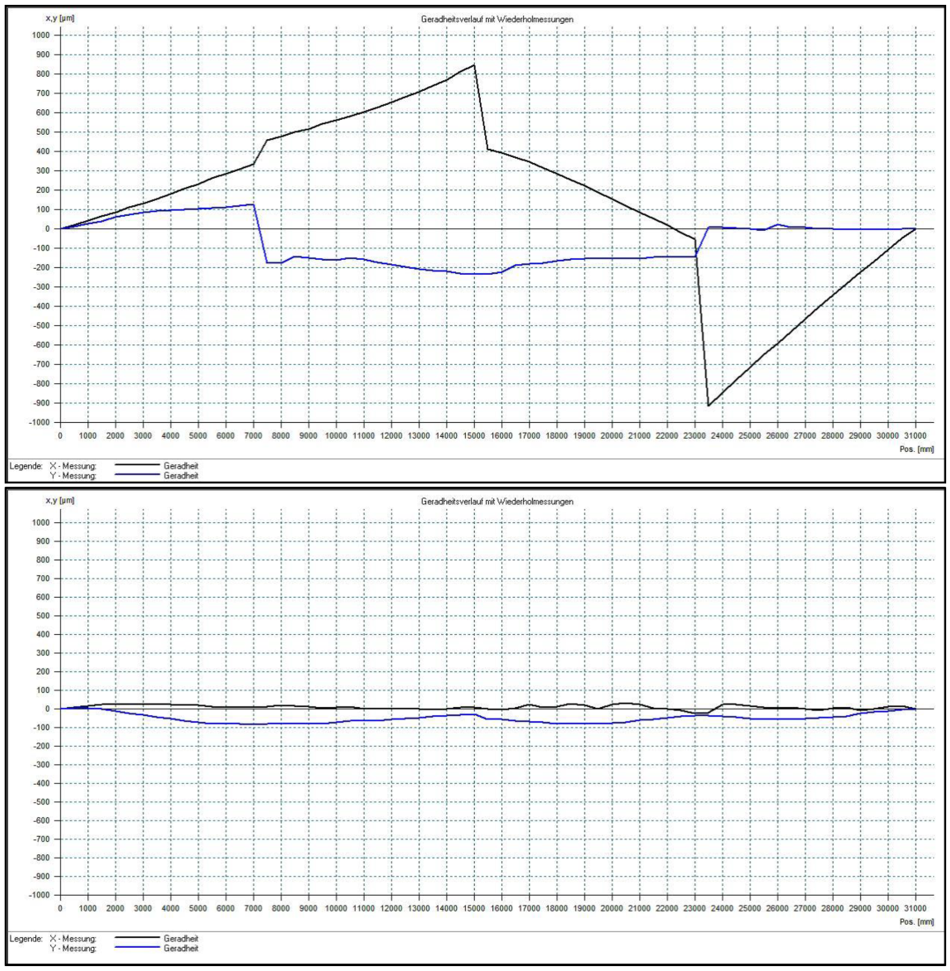
Bei Messung mit der Wasserwaage muss allerdings berücksichtigt werden, dass der Normalenvektor Richtung Erdmittelpunkt sich bei 32 m Länge bereits um 1 wsec (= 5 µm pro Meter) ändert und als Ergebnis der Neigungsmessung eine natürliche Erdkrümmung von etwa 20 µm fehlinterpretiert wird.
Erweiterung vom Winkel- zum Fluchtungsmesssystem
Das Prinzip des vignettierenden Feldblendenverfahrens lässt sich in der entsprechenden ELWIMAT®-Anordnung verwenden, um z.B. Geradheitsmessungen von Bauteilen und Führungen nach der Höhenmethode durchzuführen. Anstelle des Planspiegels wird ein Tripelspiegel verwendet (Bild 4). Das entsprechende Strahlenbündel, welches am Retroreflektor zurückreflektiert wird und wieder durch die Blende bzw. Pupille verläuft, erzeugt wie beim hier beschriebenen Verfahren mit Planspiegel den V-SPOT, welcher über die bekannte Winkelbeziehung ausgewertet wird. Über den ermittelten Winkel a und dem bekannten Abstand s zwischen Pupille und Tripel kann die seitliche Verschiebung x ermittelt werden. Mit einem zusätzlichen Reflektor, d.h. einem Doppelreflektor mit bekanntem Basisabstand b lässt sich über den gemessenen Abstand der beiden V-SPOT am Detektor der Abstand s automatisch ermitteln.
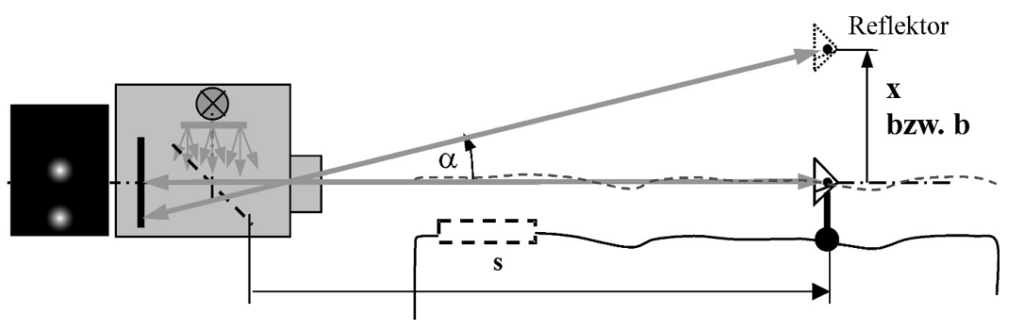
Mit dem Single-Reflektor ist damit in der Praxis mit dem hier beschriebenen Standardaufbau bei Arbeitsabstand von 0 < s < 400 mm ein Messbereich (abhängig vom Messabstand) von 1 mm bis 40 mm mit einer Reproduzierbarkeit von 0,2 µm bis 2 µm erreichbar. Die Genauigkeit der Fluchtlinie, bedingt durch die Güte der Gleichmäßigkeit der Ausleuchtung der Objektleuchtfläche, ist im genannten Abstandsbereich mit besser 5 µm zu erwarten.
Mit Hilfe eines Doppel-Tripelreflektors wie im nachfolgenden Bild 5, lassen sich weitere Freiheitsgrade bestimmen. So ist bei bekanntem Basisabstand b zweier Tripelprismen über Triangulation der Abstand s automatisch bestimmbar, indem der Bildabstand der beiden V-SPOT’s auf der Kamera ausgewertet wird. Außerdem lässt sich über die Höhenmessung beider Tripelspiegel auch der Rollwinkel als Rotation des Doppelreflektors um die z-Achse (optische Achse) ermitteln.
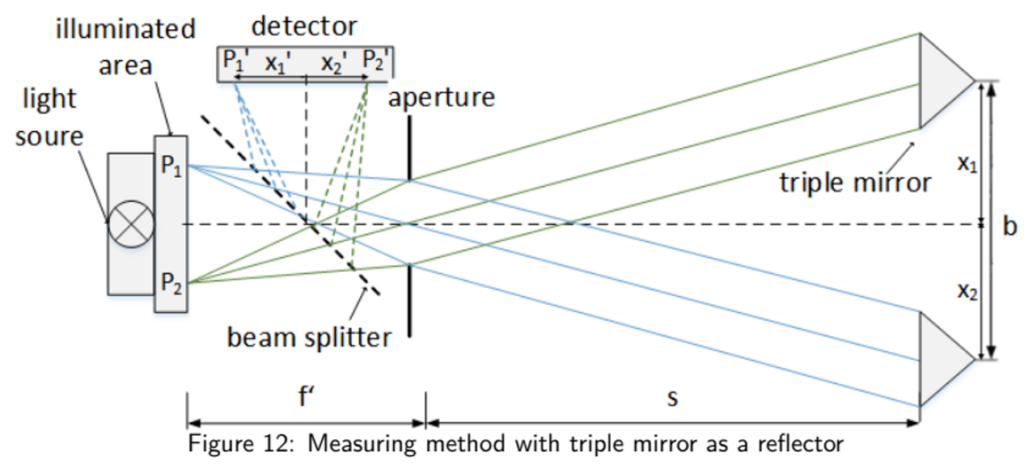
In Bild 6 ist die Anwendung des Verfahrens zur Überprüfung einer optischen Präzisions-Granitbank mit 11 m Länge gezeigt. Zur Überprüfung der Führungseigenschaften des Luftlagerschlittens sitzt der Doppel-Tripelreflektor mit zentralem Planspiegel auf diesem und verfährt. Der ELWIMAT sitzt auf einer stabilen Halterung im Vordergrund fest auf der Bank und nimmt getriggert über die Schlittensteuerung alle 6 Messdaten des jeweiligen Freiheitsgrades an jeder Position auf.

Mit einem Doppelreflektor, wie in Bild 5 skizziert und in Bild 6 zu sehen ist, nimmt der minimale Arbeitsabstand bedingt durch den endlichen Basisabstand mit 30 < b < 600 mm etwas zu. Er lässt aber auch bei Arbeitsabstand von 0,5 < s < 10 m noch eine Reproduzierbarkeit von < 10 µm und eine Genauigkeit der Fluchtlinie von ebenfalls < 10 µm erwarten. Eine weitere Erhöhung der Anzahl an Reflektoren ist denkbar, womit ebenfalls Arbeitsabstand sowie Auflösung und Genauigkeit zunehmen. Die Linearität (Messgenauigkeit der Verschiebung innerhalb einer Ebene) ist beim Doppelreflektor mit < 0,05 % des Messwertes in X-Richtung realistisch. Mit weiteren Anordnungen anderer Brennweiten und Blendendurchmesser ergeben sich entsprechende Möglichkeiten, Messbereich bzw. Arbeitsabstandsbereich und Auflösung anzupassen.
4 DoF-Messung an Spiegelsystemen
Wie in der vorangegangenen Anwendung erläutert, lässt das Verfahren zu, sowohl den Winkel als auch die Position von Spiegeln bzw. Reflektoren zu erfassen. Im vorliegenden Fall werden Laserstrahlen in einem komplexen Geräteaufbau über mehreren Strahlteiler geteilt, umgelenkt und später wieder zusammengeführt. Die Parallelität der Teilstrahlen ist im Bereich von < 10 wsec und gleichzeitig die Strahllage < 100 µm in den entsprechenden Pupillenebenen zu gewährleisten. Mit Hilfe jeweiliger Referenz-Reflektoren (Spiegel- und Tripelzielmarke) werden alternierend sowohl die Winkel als auch die Position der beiden Teilstrahlenbündel an den entsprechenden Übergabepunkten über entsprechende Stellelemente an den Teilerspiegelaufnahmen justiert und optimiert.
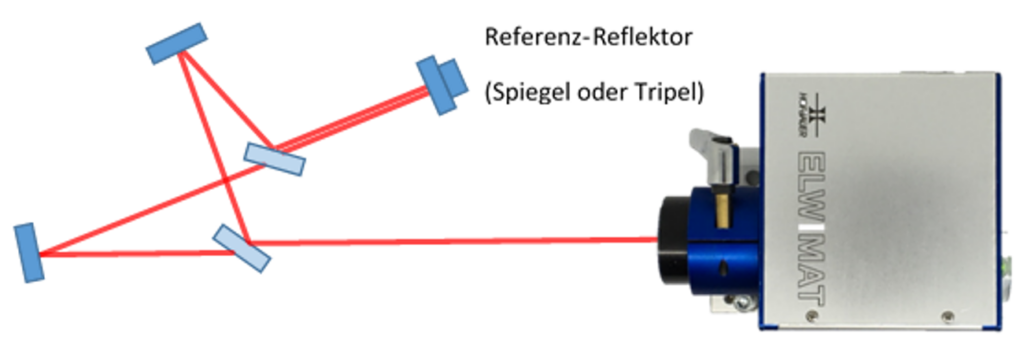
Im aktuellen Prozess werden die Referenzreflektoren (Spiegel und Retroreflektor) noch nacheinander an der Referenz-Bezugsfläche angelegt bzw. montiert, um die Winkel- und die Positionswirkung des Messprinzips zu nutzen. Dabei geht natürlich Zeit verloren. Ziel ist es in naher Zukunft, hier koaxiale Kombi-Reflektoren zu entwickeln, um die Strahlen gleichzeitig in Position und Winkel beobachten und justieren zu können.
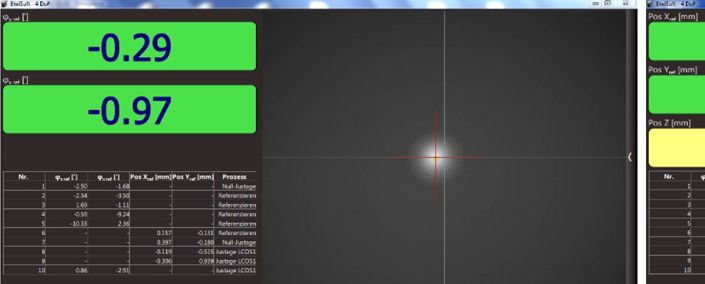

Laserstrahlenbündeln im Reinraum bei Jenoptik AG (mit frdl. Genehmigung)
5 Prismen- und Keilwinkelmessung mit V-SPOT-Verfahren
Das Prinzip der Prismen- und Keilwinkelmessung ist in Abbildung 10 skizziert. Damit lassen sich Ablenk- und Keilwinkel vor allem von größeren Keilen vermessen, welche sich – außer mit einem Absolut-Goniometer mit Teilkreis oder mit einem Relativgoniometer – mit den einfacheren herkömmlichen Verfahren der Autokollimation nicht mehr bestimmen lassen. Mit entsprechender Anordnung sind Keilwinkel bis 20 ° absolut mit der Genauigkeit im Bereich von bis zu 1×10-4 messbar und das vor allem ohne mechanische Bewegungen und ohne Referenzmessung.
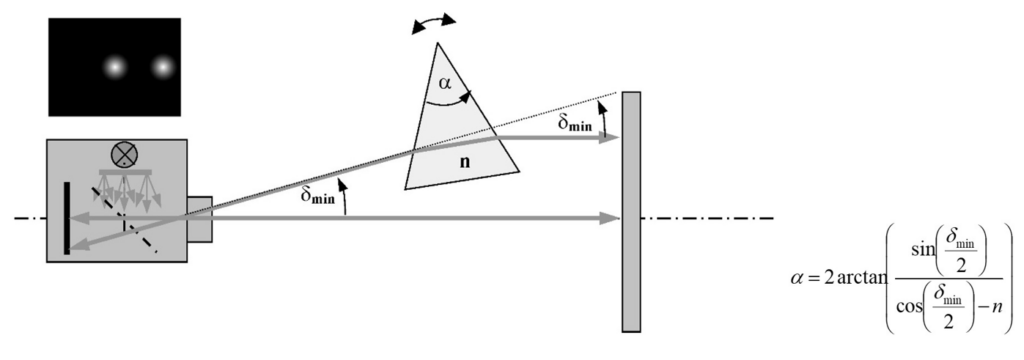
Das Referenzstrahlenbündel geht direkt auf einen Planspiegel (senkrecht) und wird zusammen mit dem abgelenkten Strahl über dem Prisma auf der Kamera erfasst und präzise auf Subpixel-Genauigkeit ausgewertet. Aus der ermittelten Winkeldifferenz der beiden abgebildeten V-SPOT’s ergibt sich direkt der Ablenkwinkel d. Über eine Rotation des Prüflings kann der minimale Ablenkwinkel dmin präzise ermittelt werden.
Somit lassen sich Prismenwinkel mit bis zu 20 Grad mit relativen Abweichungen von < 10-4 bzw. 0,01% erfassen. Ist die Brechzahl dabei ebenfalls auf besser 10-4 (± 0,0001) bekannt, kann der Prismenwinkel auf < 5 wsec gemessen werden. Bei bekanntem Prismenwinkel a, kann bei Verwendung zweier Wellenlängen mit einem ELWIMAT-DualWave auch die Brechzahl auf bis zu 10-5 sowie daraus die Dispersion und die Glassorte bestimmt werden.
6 Messung der Oberflächentopografie mit DaOS-Prinzip
Im vorangegangenen Kapitel wurde gezeigt, dass über die Winkelabweichung eines Schlittens mit Spiegel über die Oberfläche des Prüflings das Höhenprofil indirekt ermittelt werden kann. Wenn der Prüfling nun selbst über eine reflektierende Oberfläche verfügt, wie z.B. ein polierter Glaskörper oder verspiegelte Flächen, lässt sich mithilfe einer Abtast-Vorrichtung mit einem ELWIMAT® Messkopf, ein erweitertes Messprinzip entwickeln – das DaOS Prinzip (Deflectometric acquisition of Optical Surfaces) [4]. Dieses neue Verfahren fügt den im Bereich der Präzisionsoptik zur Bestimmung von Formfehlern von sphärischen oder flachen Oberflächen hauptsächlich verwendeten Verfahren der Interferometrie oder opto-mechanischen Abtastverfahren ein weiteres hinzu. Da insbesondere bei großen und dabei noch konvexen Optiken sowie bei Asphären und Freiformflächen die Verwendbarkeit und Funktionalität der Interferomtrie sehr stark eingeschränkt ist und andere opto-mechanische Abtastverfahren nicht überall verfügbar oder/und sehr kostenintensiv sind, kann unser neues Verfahren hier einen wertvollen Beitrag zur Metrologie technischer Oberflächen liefern. In den folgenden Kapiteln werden zwei Anwendungsgebiete weiter erläutert: Zum einen die Bestimmung der Oberfläche von quasi-planen großen optischen Flächen, wie sie als Substrat von Satellitenspiegeln zum Einsatz kommen können. Zum anderen wird eine Variante des DaOS-Prinzips für stark gekrümmte Flächen (sphärische oder asphärische Linsen) erläutert und anhand aktueller Messergebnisse die Anwendbarkeit des Verfahrens demonstriert.
DaOS Prinzip für quasi-plane Oberflächen
Die deflektometrische Bestimmung optischer Oberflächen beim Deflectometric Flatness Reference-Verfahren (DFR) mit einem elektronischen Autokollimator (AKF) und einem Abtast-Pentaprisma [1,2,3] hat den Hauptvorteil, dass eine relativ einfache Mechanik durch Invarianz des Strahlablenkers mit 2 Reflexionsflächen verwendet werden kann und als Absolutreferenz die Geradlinigkeit eines Lichtstrahlenbündels gilt. Damit kann auf große und teure Transmissions-Referenzflächen verzichtet und die absolute Formabweichung sehr präzise auf unter 1 nm bestimmt werden [3]. Die maximale Krümmung der zu prüfenden Oberfläche (SUT) ist jedoch durch die Vignettierung gegenüber der Länge (Durchmesser) streng begrenzt. Ein sich änderndes Krümmungsvorzeichen beeinflusst ebenfalls die Abbildung des Fadenkreuzes bei einem AKF dramatisch und die Auswertung der Winkelmessung ist möglicherweise nicht erfolgreich [4].
Aufbau der Mess-Apparatur beim DaOS-Verfahren
Durch die Verwendung des ‚Vignetting Field Stop‘ (VFS)-Verfahrens anstelle des klassischen AKF ist die Vignettierung kein Problem mehr, sondern eine einfache Lösung zur Messung sehr großer Winkel. Einer der emittierten Strahlenbündel innerhalb des divergenten Strahlenbüschels steht immer senkrecht zur Oberfläche und wird daher direkt zum Sensor zurückreflektiert und verläuft durch die Apertur der Optik. Anstelle eines scharfen Bildes wird ein mathematisch klar beschreibbarer, defokussierter Lichtfleck bestimmt [5]. Damit sind auch nicht-plane oder nicht-sphärische Flächen wie Asphären und Freiformflächen prinzipiell messbar. Die V-SPOT-Abweichungen werden erfasst und ein präzises Bildverarbeitungsverfahren berechnet den Wert des seitlichen Versatzes entsprechend dem Winkel des reflektierten Strahls. Die Neigungswinkeländerungen werden über Integration zu Höhenwerten bestimmt und die Oberflächentopografie über mathematische Verfahren rekonstruiert. Die Lage und Dichte der Abtastschnitte kann dem Prüfling und der Prüfvorgabe angepasst werden.
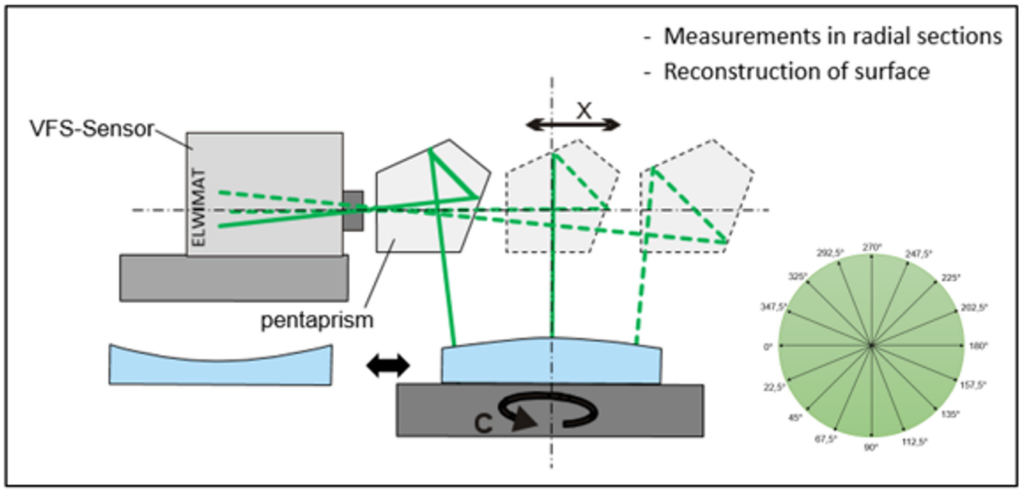
Rekonstruktion der optischen Oberfläche aus den Linien-Scans
Für einen direkten Vergleich der Messungen am Interferometer werden die Ergebnisse der Winkelmessung durch einen mathematischen Algorithmus auf Höhenabweichungen pro Ortspunkt berechnet (siehe dazu Bild 12).
Um die Oberfläche eines Spiegelsubstrats zu rekonstruieren, werden mehrere radiale Schnitte unter Verwendung von Linienscans in azimutalen Schnitten gemessen – je mehr Scans, desto besser wird die Rekonstruktion. Die beste Strategie unter Berücksichtigung von Zeit, Temperaturschwankungen und Rekonstruktionsgenauigkeit ist abhängig von den Umgebungsbedingungen und den Anforderungen an die zu erzielende Genauigkeit.
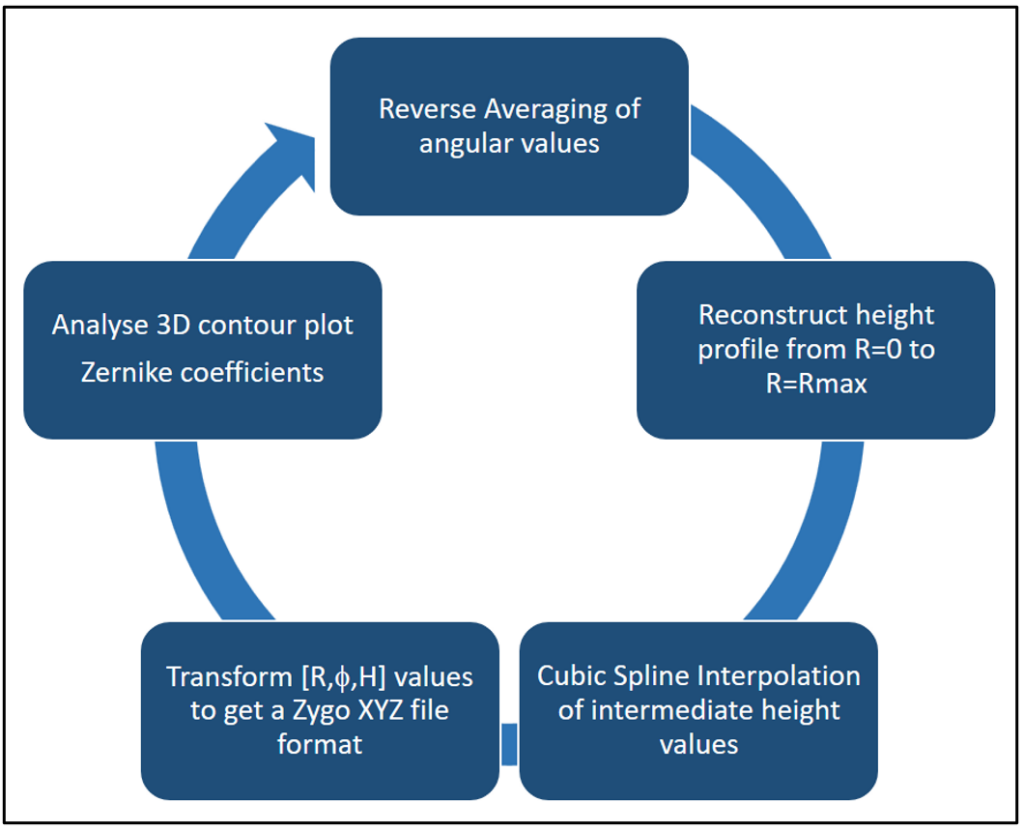
In einem ersten Schritt werden die Winkelwerte von Schnitt 1 bei einem Winkel a und bei a + 180° normiert und entgegengesetzt addiert (Reverse-Messung), um eine etwaige nichtlineare Temperaturdrift zu kompensieren [8].
In einem zweiten Schritt werden die Winkelkurven von R=0 bis Rmax integriert. Dies stellt sicher, dass alle Kurven bei R=0 den Wert Null haben.
In einem dritten Schritt werden die Höhenkoordinaten in Polarform in eine kartesische Form umgerechnet. Dazu werden die Winkel- und Radial-Werte interpoliert (Cubic Spline), um eine ausreichende Datendichte in (X,Y) zu erreichen.
Die kartesichen Werte werden in ein (x, y, z) Format übertragen und nach ZYGO eingelesen. Dort können Sie mit den interferometrischen Profilen verglichen werden.
Fehlerabschätzung – Unsicherheitsbudget
Es gibt einige Einflüsse bei Messabweichungen, die berücksichtigt und beseitigt oder reduziert werden können, um eine Genauigkeit im Bereich von l/10 @633 nm zu erzielen.
Häufige Abweichungen wie thermische Drift, Vibrationen, geometrische Abweichungen und Penta-Wellenfrontfehler sind für diesen Instrumentenaufbau wichtig. Es gibt jedoch zusätzliche systematische Effekte, unbekannte systematische Abweichungen und zufällige Abweichungen, die Einfluss auf die Unsicherheit einer Messung haben.
Einerseits können mehrere zufällige Abweichungen wie Vibrationen und Luftturbulenzen, Sensorsignalverarbeitung (Signal-Rausch-Verhältnis) und nicht wiederholbare Rollwinkel-Abweichungen der linearen Bewegungsachse geschätzt, aber kaum vermieden werden. Andererseits gibt es systematische Abweichungen wie Temperaturgradienten in der Messumgebung und am Prüfling, geometrische Abweichungen, Pentaprismeneinstellung und Wellenfrontaberrationen, Linearität des Sensors und abstandsabhängige Auswirkungen auf den V-SPOT-Sensor. Diese Abweichungen können in einem optimierten Aufbau und sogar in unserer Inline-Messdurchführung auf einer Hebelpoliermaschine durch Vorwärts- und Rückwärtsmessungen kompensiert oder minimiert werden [4]. Es bleiben jedoch unbekannte systematische Restabweichungen, die geschätzt und in Tabelle 1 gezeigt werden. Die Unsicherheit bei der Profilbestimmung als Maß für die maximale Durchbiegung in Bahnmitte [9,10,11], ist ein wichtiger Einfluss, den wir hier berücksichtigen. Er wird für jeden Anteil der rms Winkelwerte in der Tabelle ermittelt.
Wir können die Genauigkeit durch kleinere Schritte auch auf sehr großen Flächen erhöhen. Im Einzelnen gehen Größen wie das Winkelauflösungsvermögen des VFS-Sensors, die Schrittweite und die Messlänge (Prüflingsdurchmesser) ein [11].
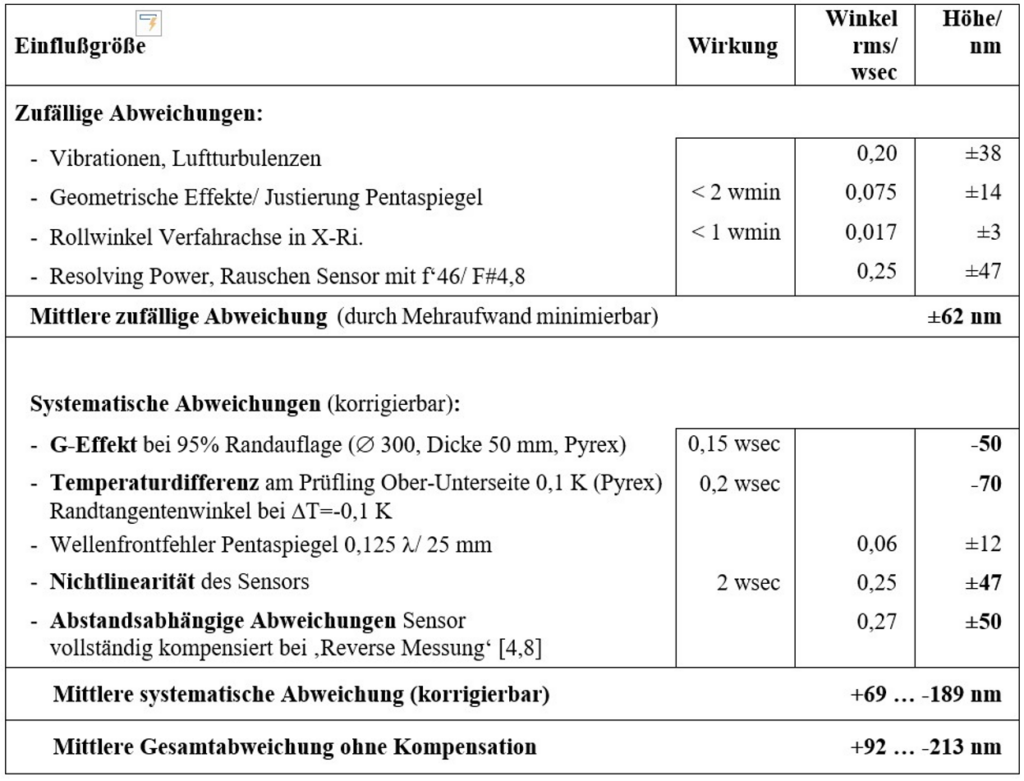
Bei unkompensierten Einflüssen der in der Tabelle genannten Größen auf die Messung ergibt sich im vorliegenden Fall eine mittlere Gesamtabweichung von +92 bis -213 nm. Die größten Einzeleinflüsse aus Tabelle 1 sind systematischer Natur und korrigierbar:
Erstens die Temperaturdifferenz am Prüfling bei ungünstigem Wärmeausdehnungskoeffizienten, zweitens der G-Effekt durch Schwerkrafteinfluss bei horizontaler Prüflingslage sowie drittens Abweichungen durch Nichtlinearität aus entfernungsabhängigen Sensorfehlern. Bei gekrümmten Flächen (ca. 3 m < R < 100 m) ist ein Skalierungsfaktor für den Schrittabstand zu berücksichtigen. Dies erfordert eine nichtlineare Kartentransformation in x-Richtung, auf die hier aber nicht näher eingegangen wird. In der weiteren Diskussion nehmen wir an, dass der Prüfling ausreichend flach ist, um den Skalierungsfaktor zu vernachlässigen.
Validierung mit einem „Plan-Doppel-Sombrero“
Um das Messprinzip des neuen DaOS zu validieren, wurde zunächst eine spezielle „plan-asphärische“ Geometrie mit „Doppel-Sombrero“ auf einem Substrat (Pyrex) mit 300 mm Durchmesser und 50 mm Dicke erstellt und durch einen kurzen Round-Robin-Test mit interferometrischen und DFR-Methoden gemessen [4].
Für die interferometrischen Messungen wurde ein QED SSI-A-Instrument mit einer 4”-TransmissionFlat TF und einer 6”-TF verwendet – beide wurden vorher mit einem Dreiplattentest am TC Teisnach kalibriert. Eine weitere Bewertung liefert ein 12-Zoll-Fizeau-Interferometer in vertikaler Mess-Position bei Berliner Glas. Der Prüfling liegt dabei horizontal, ebenso wie die 305 mm große Referenz-Fizeaufläche. Die deflektometrischen DFR-Messungen wurden mit klassischen elektronischen Autokollimatoren mit Fadenkreuz dreier verschiedener Hersteller (MÖLLER-WEDEL, Trioptics, HOFBAUER OPTIK) in 4 Schnitten bei 0°, 45°, 90° und 135° durchgeführt und mit Rekonstruktionssoftware-Algorithmen (bicubische Splineinterpolation) ausgewertet [4].
Bild 13 zeigt das Ergebnis der Interferometer-Messung am 12 Zoll-Interferometer.
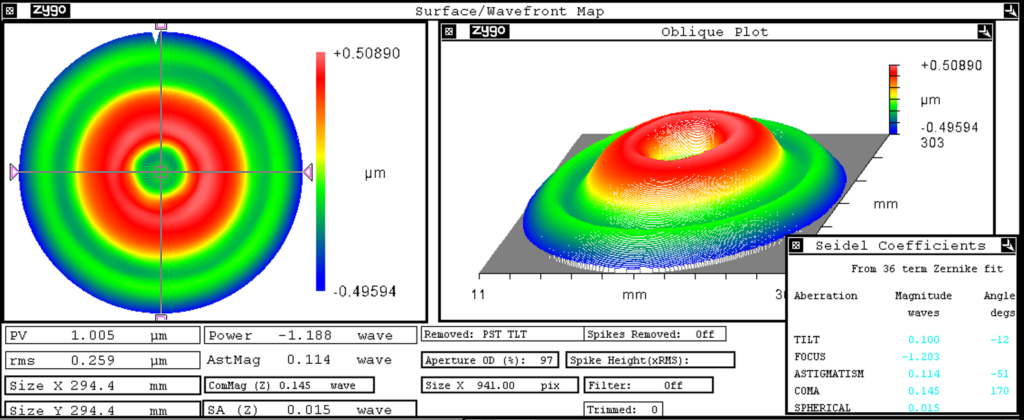
Tabelle 2 enthält zusammengefasst die PV-, Rms- und SAG-(Power)Werte für alle Interferometer und die DFR-Messungen mit dem Autokollimator.
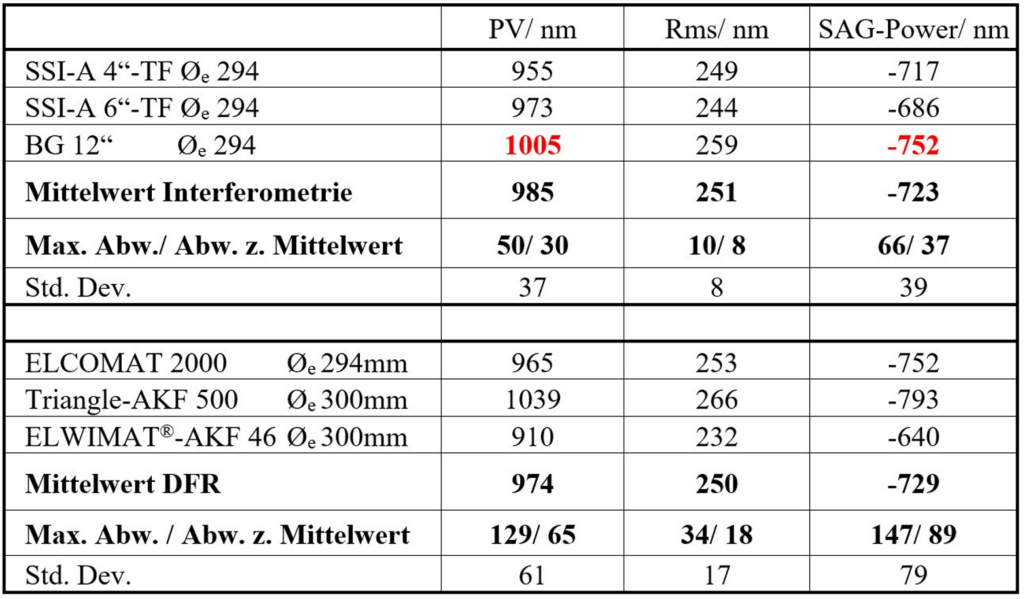
Die in Tabelle 2 gezeigten Ergebnisse zeigen bei den drei interferometrischen Messungen in zwei verschiedenen Labors und zwei verschiedenen Interferometertypen einen durchschnittlichen PV-Wert von 985 nm mit einer maximalen Abweichung von 50 nm. Die absolute Abweichung der 3D-angepassten Power (SAG-Abweichung) liegt hier bei maximal 66 nm. Die Standardabweichung des Mittelwerts der drei Messergebnisse beträgt 39 nm. Die größere Abweichung am Instrument bei Berliner Glas mit PV 1005 nm bzw. SAG (Power) 752 nm ist ein durch die Schwerkraft zusätzlich induzierter G-Effekt, da die Transmissionsreferenzfläche aufgrund der vertikalen Interferometer-Anordnung eine zum Zeitpunkt der Auswertung noch nicht verifizierte und kompensierte Verformung von bis zu 50 nm im Power-Term aufweist.
Die DFR-Messungen im Vergleich dazu liegen im Mittel sehr gut am Mittelwert der interferometrischen Messungen (Abweichung dazu 11 nm PV bzw. 6 nm SAG). Allerdings streuen die DRF-Messungen mit einer max Abweichung von PV 129 nm bzw. 147 nm um mehr als Faktor 2 deutlicher als die interferometrischen Messungen mit 50 bzw. 66 nm.
Als wesentliche Ursachen können wir diesbezüglich zum geringen Anteil einen möglichen Proportionalitäteffekt der unterschiedlichen Autokollimatoren (Linearitätsfehler) sowie im Wesentlichen die Temperaturgradienten an den jeweiligen Messapparaturen verantwortlich machen. In den Feinmessräumen (sowohl TC Teisnach, als auch Berliner Glas) herrschen sehr gute Temperaturbedingungen (21,5° C +/- 0,2°C) im Gegensatz zum Labor 5, in dem die DFR-Messungen durchgeführt wurden und 1 bis 2° C Tagesschwankung gegeben sind. Hier ist aufgrund der Materialbedingungen mit hohem thermischen Ausdehnungkoeffizienten (Pyrex) eine deutlichere Variation zu erwarten und sichtbar. Ein Blick auf Tabelle 1 zeigt eine mittlere Gesamtabweichung von +92 … -213 nm, in dem sich die Schwankungsbreite von 147 nm ziemlich gut wiederfindet und dem vorhergesagten Unsicherheitbetrag gut annähert. Um einen Einfluss von unterschiedlichen Rekonstruktionsalgorithmen bei der 3D-Rekonstruktion zu vermeiden, reduzieren wir die Datenanalyse auf eindimensionale 2D-Messungen für den Zeilenscan. Bild 14 zeigt die Schnitte für zwei der interferometrischen sowie die der deflektometrischen DFR-Messungen mit AKF in Azimutrichtung von 0 Grad.
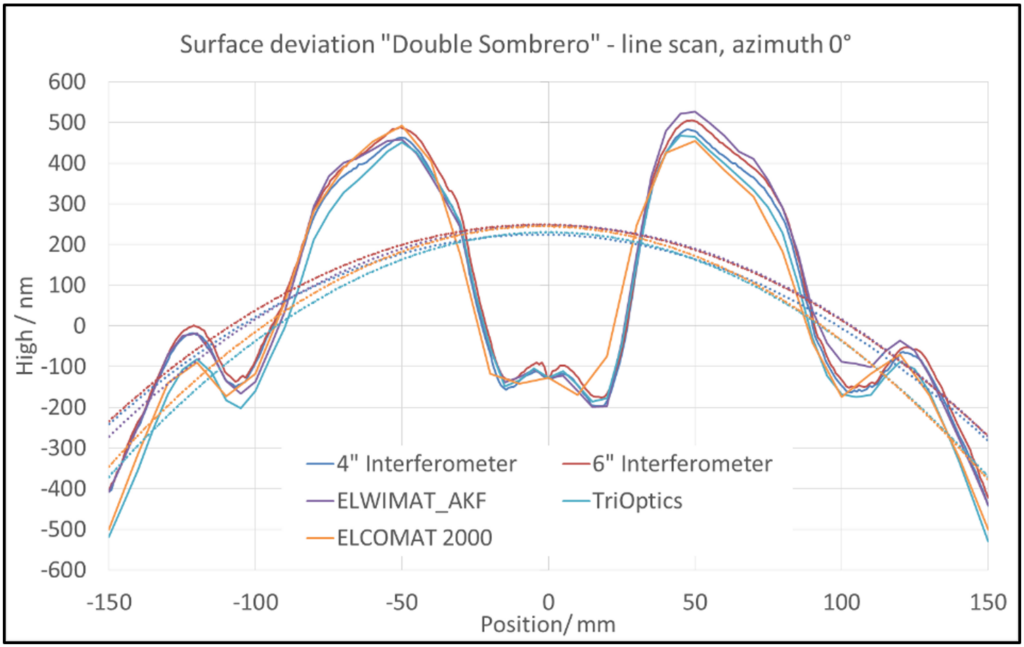
Es besteht eine gute qualitative Übereinstimmung hinsichtlich der Struktur des sogenannten „Doppel-Sombrero“. Es ist aber auch zu sehen, dass alle Messungen in der Sagittahöhe etwas variieren. Die Power-Anteile (SAG) im 2D-Schnitt bei 0° sind als sphärischer Anteil ebenfalls in der Grafik dargestellt und unterscheiden sich um bis zu 112 nm. Diese werden im nächsten Schritt (Abbildung 16) von den Ergebnissen abgezogen, um die Einflüsse aus der mangelnden Temperaturkonstanz bzw. die Effekte des Temperaturdehnungskoeffizienten des Prüflings von der eigentlichen Messtechnik zu eliminieren.
DaOS-Messungen an Doppel-Sombrero mit V-SPOT-Sensor
Zur Bewertung des Verfahrens mit dem neuen V-SPOT-Sensor werden nun im Vergleich zu den vorherigen Referenzmessungen die Messungen mit dem Vignettierenden Feldblenden-Sensor ELWIMAT 46-4,8 UI1542#19 (Bild 15) mit einer Brennweite von 46,1 mm bei F #4,8 betrachtet. Die Messungen werden in Linienscans bei 0 Grad am Doppel-Sombrero durchgeführt. Die meisten nichtlinearen systematischen Abweichungen wie Penta-Prismen-Wellenfrontfehler und Abstandsabhängigkeitsfehler des gesamten DaOS-Aufbaus werden durch Umkehrmessung reduziert. Das Messergebnis der DaOS-Messung mit dem V-SPOT-Sensor ist neben den Referenzmessungen (Interferometer und DFR) in Abbildung 16 dargestellt. Die Endergebnisse für PV, Rms und Power sind in Tabelle 3 aufgeführt und zeigen eine sehr gute Übereinstimmung aller drei Messarten.

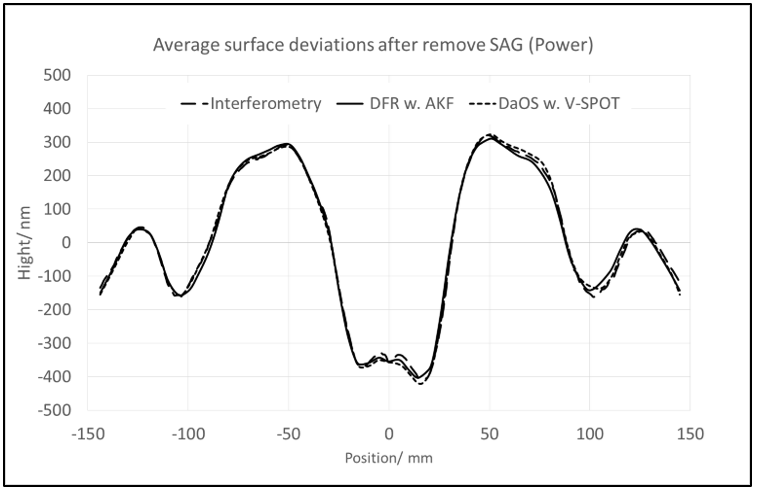
In Tabelle 3 sind die Ergebnisse numerisch dargestellt. Die maximale Abweichung im Schnitt bei 0° beträgt 29 nm PV und 4,6 nm rms.

Die Abweichungen zum Mittelwert der Referenzmessungen (Mittelwert der Ergebnisse aus Interferometerie und DFR mit AKF’s) liegen bei 22,5 nm PV und 4,6 nm rms und stellen ein beachtliches Ergebnis dar.
Direkter Vergleich der Messdaten aus 2D-Zeilenmessung
Zum direkten Vergleich der Daten und zur Berechnung der Kurvendifferenzen werden die geringeren Datenmengen der DaOS-Messungen interpoliert. Anschließend nehmen wir die Residuen der jeweiligen Messungen von DaOS zu den interferometrischen Messungen. Es zeigt sich, dass bei den DaOS-Messungen im Vergleich zur Interferometrie Abweichungen von
PV = 54 nm / rms = 11,0 nm auftreten. Das Ergebnis ist grafisch in Bild 17 dargestellt.
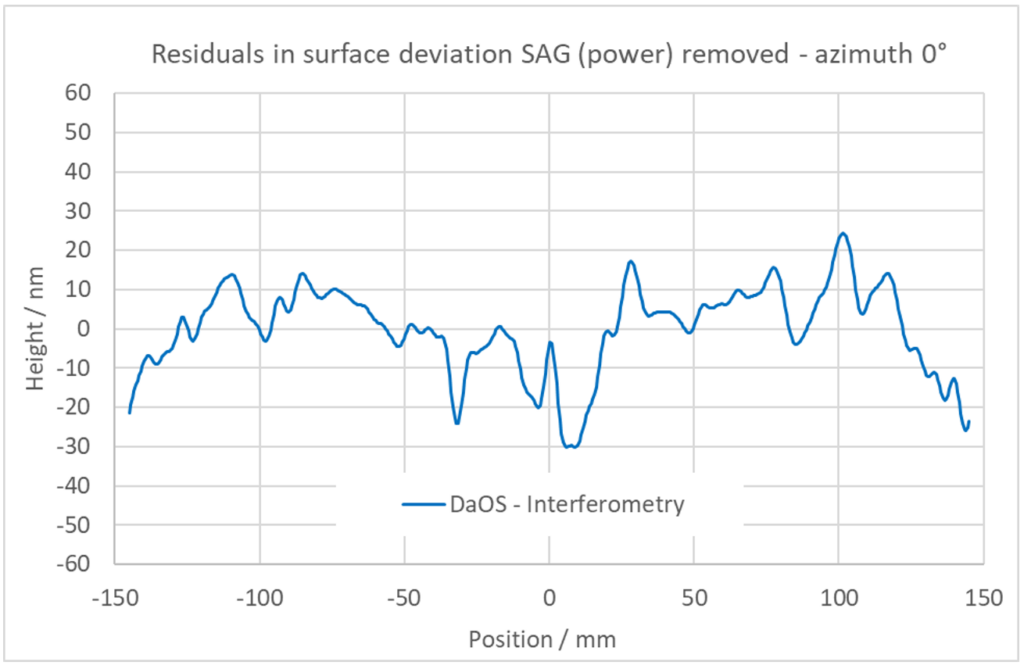
In Anbetracht des Sagittafehlers (SAG) von bis zu 112 nm können wir im Wesentlichen Temperatureffekte durch unterschiedliche Temperaturgradienten am Prüfling feststellen, welche eine sphärische Krümmung erzeugen (Bi-Metall-Effekt). Diese sind an den verschiedenen Messorten unterschiedlich und bei der ungünstigen Materialwahl von Pyrex deutlicher höher als die jeweiligen Messunsicherheiten des Messverfahrens.
Die sich ergebenden Messabweichung des Höhenprofils beim DaOS-Verfahren mit neuem V-SPOT-Prinzip durch Restfehler wie Luftturbulenzen, Sensorrauschen und Sensorgrenzauflösung sowie Linearitätsabweichungen des Sensors im Bereich von jeweils unter 1 Winkelsekunde liegen damit, wie Abbildung 17 zeigt, im Bereich von etwa +/- 30 nm oder PV 54 nm.
Im Vergleich zu interferometrischen Stichingergebnissen mit SSI-A und einem 12-Zoll-Fizeau-Interferometer bei Berliner Glas konnten wir zeigen, dass es möglich ist, systematische Abweichungen höherer Ordnung (Nichtlinearität und Prismenwellenfrontfehler) des Setups von DaOS zu kompensieren sowie mechanisch-thermische Abweichungen durch Simulation und Kalibrierung zu korrigieren. Dabei erreichen wir auch bei großen Optiken von 300 mm bessere Ergebnisse als IRR < 60 nm entsprechend l/10 und rmsi < 11 nm entsprechend l/50 @633 nm.
7 Messung des Abtragsverhaltens – In-Situ Messung an NLP 500
Nachdem im vorigen Kapitel gezeigt wurde, dass mithilfe des DaOS-Verfahrens eine optische Oberfläche hinreichend – i.e. IRR l<60 nm gemäß l/10 PV – gut charakterisiert werden kann, wurde das Verfahren zur Insitu-Messung des Polierprozesses an einer Hebelpoliermaschine Stock NLP-500 eingesetzt [13]. Der gesamte Aufbau und die Messungen wurden im Rahmen eines ZIM-Projektes verwirklicht [ZIM DoSuRe, 2016-2018].
Die Traverse besteht aus einer Linearachse mit Servomotor und Controller, einem VFS Sensor der Fa. HOFBAUER OPTIK (Elwimat 46-4.6) sowie einem Penta-Spiegel hoher Qualität. Die Ausrichtung des Scans erfolgt über eine Vorabmessung, damit alle Scans für verschiedene Winkel durch den Mittelpunkt der Probe gehen. Die Ansteuerung des Motors und die Datenerfassung erfolgt synchron über eine speziell entwickelte Software.

Der Durchmesser des Strahlenbündels auf der Probe (Footprint) entspricht ca. 5 mm – d.h. Strukturen, die kleiner als 5 mm sind, werden gedämpft. Es werden 16 Schnitte durchgeführt. Die Schrittweite pro Datenpunkt beträgt 5 mm. Die gesamte Messzeit liegt bei etwa 70 min. Das Glassubstrat (Pyrex) hat einen Durchmesser von 310 mm und eine Mittendicke von 45 mm. Die zu untersuchende Oberseite ist nahezu flach (R > 4 km) und wird im Laufe der Untersuchung mehrmals bearbeitet. Die Unterseite ist konkav (R~-1500 mm, Sag-Höhe ~ 8 mm), ebenfalls poliert jedoch ablackiert, um Rückseitenreflexe zu minimieren. Ziel des Projektes war die Insitu-Charakterisierung verschiedener Polierschritte. Dazu wurde die gesamte Oberfläche vermessen und mit den 3D-Messungen an einem Interferometer verglichen.
Das Interferometer war ein QED SSI-A, welches am Standort Teisnach zur Verfügung stand. Alle Messungen nach dem DaOS-Prinzip wurden unter „Shop floor“ – Bedingungen gemacht, was heißt, dass es keine aktive Regelung der Umgebungsbedingungen (Temperatur, Vibrationen, usw.) gab. Die interferometrischen Messungen wurden im kontrollierten Messraum (dT < 0,1 K/ h) durchgeführt.
Polier- und Mess-Prozedur
Für einen detaillierten Vergleich der Oberflächen mit dem Interferometer und dem Deflektometer-Messgerät wurde folgende Sequenz aus Polier- und Mess-Schritten durchgeführt (siehe Bild 19):
Das Glassubstrat wurde in einem vorbereitenden Schritt auf ein definiertes Startprofil hin poliert, welches einem einfachen „Sombrero“ gleicht. Nach diesem Polierschritt wurde die Probe sowohl im Interferometer (dazu wurde das Substrat demontiert und ins Messlabor verbracht), als auch deflektometrisch in der Poliermaschine vermessen (M1).
Danach folgte quasi ein erster Abtrags-Polierschritt, der hauptsächlich den Rand des Substrates abgetragen hat (PV reduziert von ca. 2µm auf 1 µm). Nach diesem Polierschritt erfolgte die zweite Messung am Interferometer und an der Poliermaschine (DaOS). Nach der Messung erfolgte ein zweiter Abtrags-Polierschritt, der den inneren Bereich abgetragen hat.
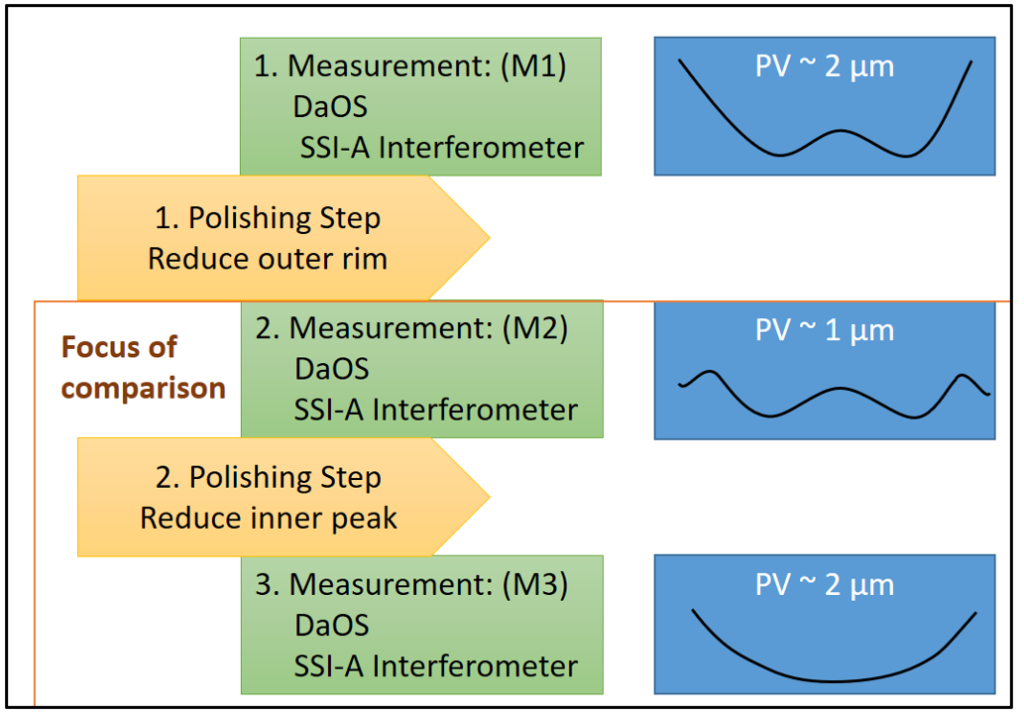
Dieser Schritt wurde in der dritten Messung (M3) charakterisiert.
Zwischen den Arbeitsschritten (Polieren, Messen am Interferometer, Messen an der Poliermaschine mit DaOS) lagen einige Tage, so dass wir davon ausgehen können, dass thermische Effekte durch den Poliervorgang auszuschließen sind.
Der Fokus der Bewertung liegt auf dem zweiten Abtrag der Poliermaschine.
Vergleich des Abtrags beim Polieren
Das folgende Kapitel zeigt die Ergebnisse der Messungen für den Abtrag des 2ten (?) Polierschrittes. Zum Vergleich mit der Kontur aus den interferometrischen Messungen wurde die Oberfläche – wie im Kapitel „Rekonstruktion der optischen Oberfläche“ beschrieben -rekonstruiert aus den Linienscans und als Kontur ausgegeben.
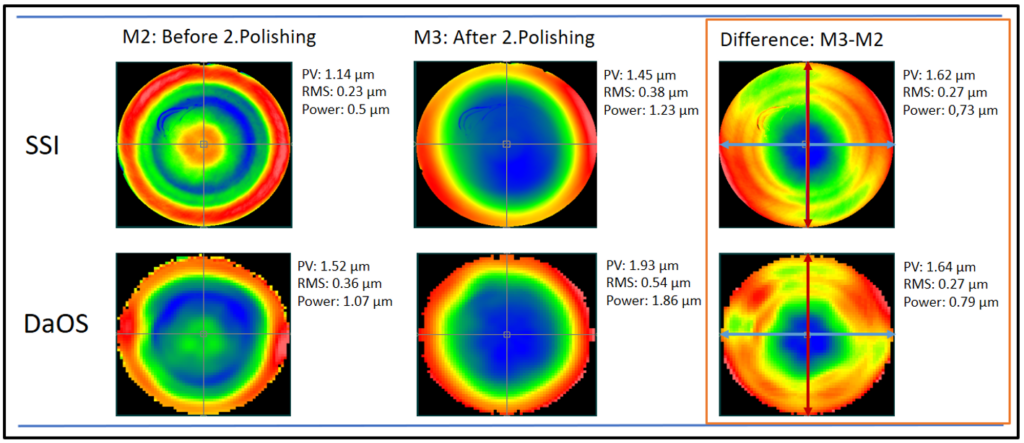
Im Allgemeinen gilt, dass bei einer visuellen Inspektion des Konturplots (Abb. 20) eine hinreichend gute Vergleichbarkeit zwischen SSI und DaOS besteht. Wenn man genauer hinsieht, erkennt man jedoch zum einen Astigmatismus bei der Interferometermessung sowie eine Abweichung im Power-Wert bei den absoluten Messungen M2 und M3 der DaOS-Messungen von ca. -500 nm.
Die Ursache dafür ist zum einen ein Power-Anteil von etwa 100 nm durch den G-Effekt bei überwiegender Randauflage durch die stützenden Soft-Pads aufgrund der Hohlfläche der Rückseite des Prüflings (Simulation mit GuiPlop-Software).
Die restliche Abweichung wird voraussichtlich hervorgerufen durch die Wärmequelle Antriebsmotor an der Werkstückspindel, welche u. U. eine Temperaturdifferenz von bis zu 0,5° C (Ober- zu Unterseite) hervorruft und damit eine Durchbiegung bei gegebenem Material mit hohem Dehnungskoeffizienten von Pyrex etwa -400 nm erzeugt. Der Prüfling ist zwar ausgetempert, aber die Spindel selbst ist bei der Messung in Betrieb und erzeugt und leitet die Wärme nach oben zum Prüfling, der oben auf dem Teller liegt.
In der Differenz-Auswertung ist dieser zusätzliche konstante Power-Anteil nicht sichtbar, was die Übereinstimmung von SSI und DaOS in der Abtragsverhaltens-Betrachtung wesentlich besser macht. Rein numerisch verglichen, ergibt sich ein DPower von ~ 60 nm, ein DPV von ~ 20 nm und ein DRMS von ~ 5 nm. Natürlich ist dieser Vergleich nicht wirklich aussagekräftig, da sich PV-Werte innerhalb zweier Messkurven nicht grundsätzlich überdecken und auch nicht zwingender Weise das gleiche Vorzeichen haben. Um die tatsächlichen Unterschiede im Direktvergleich der 2D-Daten besser bewerten zu können, wurde deshalb, wie bereits im letzten Abschnitt, entlang der X-Achse und der Y-Achse das Schnittbild über Residuumbildung verglichen (siehe Bild 21).
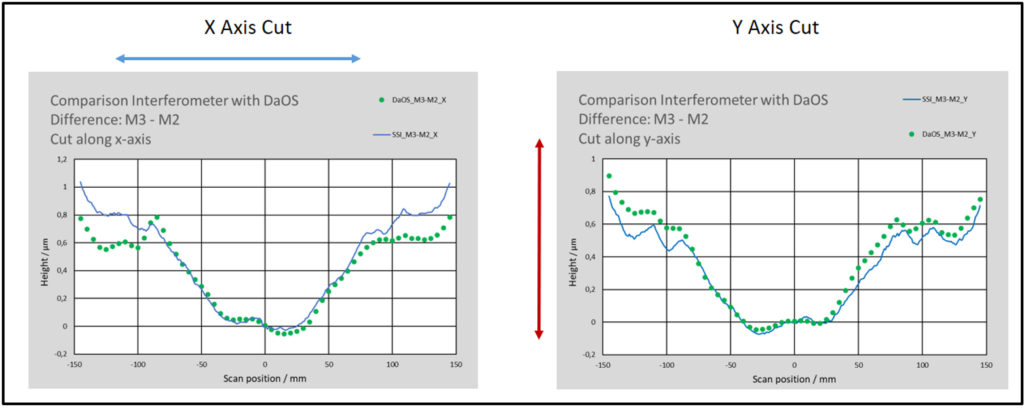
Im inneren Bereich (-100 mm < x,y < 100 mm) ist die Konformität sehr hoch. Die Abweichung beträgt maximal 50-60 nm (i.e. l/10 @633 nm). Im äußeren Bereich ist die Abweichung deutlich größer (345 nm, i.e. l/2 @633 nm).
Um ein vollständiges Bild der Unterschiede zu bekommen, zeigt das Bild 22 die Differenz zwischen Interferometer und DaOS als Konturplot.
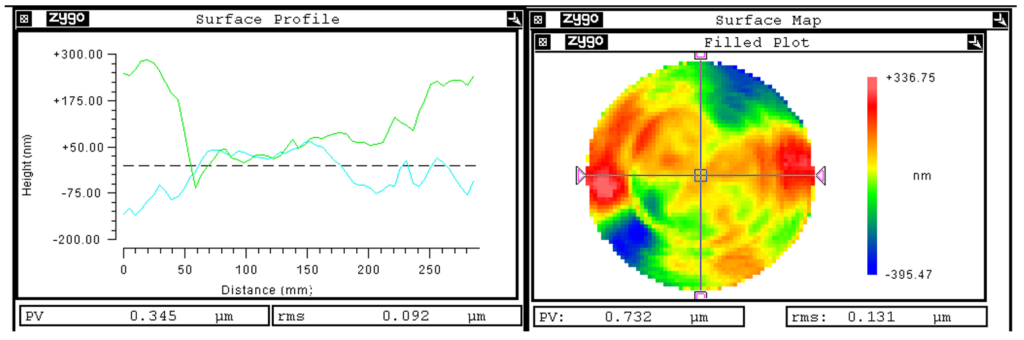
Wie schon vorher in den Schnittbildern, ergibt sich eine relativ flache Kontur im inneren Bereich (l/5 @633 nm über die ganze innere Oberfläche) und eine punktuell stark abweichende Kontur im Außenbereich (~ l @633 nm). Was zum gegenwärtigen Zeitpunkt leider nicht bekannt ist, ist die Tatsache, wie der astigmatische Unterschied bei den Interferometermessungen zustande kommt (evtl. fehlerhafte Auflage bei einer der SSI-Messung über vorzugsweis nur zwei statt 3-Punkt-Auflage. Weitere Untersuchungen sollen anschließen, um über eine zusätzliche zirkulare Kreismessung uneindeutigen nichtrotationssymmetrische Verkippungen durch z.B. Coma, Trifoil usw. sowie thermische Einflüsse während der Messung zu erfassen.
Als Zusammenfassung kann man attestieren, dass mit der DaOS-Methode eine sehr gute Übereinstimmung von < l/10 PV und < l/50 rms mit der interferometrischen Messung bei der Oberflächenrekonstruktion an großen Prüflingen von z.B. 300 mm Durchmesser erzielt werden kann. Bei der In-Situ Mesung kann das Abtragsverhalten ebenso präzise prozessiert werden und über eine einmalige Vergleichsmessung die Anlage quasi kalibriert werden. Allerdings korreliert die Genauigkeit und Vergleichbarkeit der Ergebnisse stark mit den Umgebungsbedingungen und der Materialwahl des Prüflings. So lässt sich z.B. bei Pyrex nur mit großem Kompensationsaufwand eine gute Formrekonstruktion erwarten. Bei Quartz- oder Zerodurprüflingen dagegen sind die Temperatureinflüsse deutlich geringer oder vernachlässigbar.
8 DaOS Prinzip für stark gekrümmte Oberflächen 1 mm < R < 4000 mm
Im vorherigen Kapitel wurde das DaOS-Prinzip auf quasi-plane Oberflächen angewendet. Aufgrund der linearen Messanordnung und der Limitierung des maximalen Akzeptanzwinkels (bei Brennweite fobj = 46 mm entspricht dies ca. ± 3°) können mit diesem Prinzip nur schwach gekrümmte Oberflächen (Krümmungsradius > 4 m bei Æ 300mm, entspricht > F#7,5) vermessen werden.
Für kleinere Linsen oder Asphären, deren Krümmungsradien im Zentimeter-Bereich liegen, ist das DaOS-Prinzip in einem geänderten Aufbau im Einsatz.
Aufbau der Mess-Apparatur
In den folgenden Bildern ist das Mess-Prinzip und ein Mess-Aufbau erläutert:

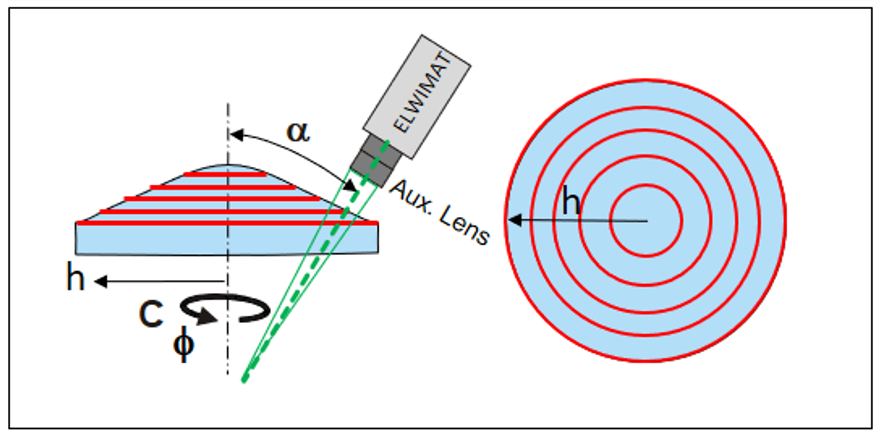
Um gekrümmte Oberflächen zu vermessen, kommt eine Vorsatzoptik mit Blendenfunktion zusätzlich zur Optik des Messkopfes zum Einsatz. Damit verringert sich der Abtast-Durchmesser („footprint“) der Blende um den Faktor fVorsatz/R0. Bei kleinstmöglicher Blende (Æ ~ 1,4 mm) erreichen wir einen effektiven footprint von ca. 160 µm [14].
Messgrößen und Messauswertung
Analog zur vorherigen Methode wird auch hier die Winkelkomponente in Scanrichtung ausgewertet (sagittale Winkelkomponente). Die meridionale Winkelkomponente wird zwar auch aufgenommen, kann aber aufgrund der unpräzisen Bestimmung des Neigungswinkels a (Da~0,5°) nicht mit der notwendigen Präzision ermittelt werden. Ein neues Projekt mit der Hochschule Deggendorf wird diesen baulichen Nachteil eliminieren und im Folgenden auch eine präzise Bestimmung der meridionalen Komponente und damit die Vermessung der radialen Form in höchster Präzision erlauben.
Ein Vollkreis entspricht in unserem Aufbau etwa 300-600 Einzelpunkten, wodurch sich eine zunehmende Schrittweite zum Rand hin von max. 0,3 – 0,15 mm ergibt für die im folgenden gezeigten Ergebnisse an den HLEM#3 Linsen (Æ = 30 mm). Eine Schrittweite, die deutlich kleiner als der footprint ist, erlaubt keine bessere Auflösung, aber verlängert die Messzeit unnötig.
Neben der Rekonstruktion der Oberfläche, die leicht abgewandelt (statt radialen Schnitten werden zirkulare Schnitte rekonstruiert) hier auch Anwendung findet, kann eine spektrale Analyse des Slope Errors wichtige Erkenntnisse zum Herstellungsprozess liefern. Hierbei zeigt sich die Stärke der Methode bei der Analyse der mittelfrequenten Fehler (MSFE) beim Herstellungsprozess [12,14].
Eine vollständige Rekonstruktion der Oberfläche erlaubt wieder den Vergleich mit interferometrischen Methoden und zeigt die Genauigkeit der Profilmessung mit dem DaOS Prinzip. Wie bereits oben angedeutet, kann in diesem Aufbau die Form (Sphärische Form, asphärische Parameter) nicht bestimmt werden. Aber die Formabweichungen werden in sehr guter Qualität mit einem durchaus kostengünstigen Verfahren bestimmt.
DaOS-Messsungen an Asphären
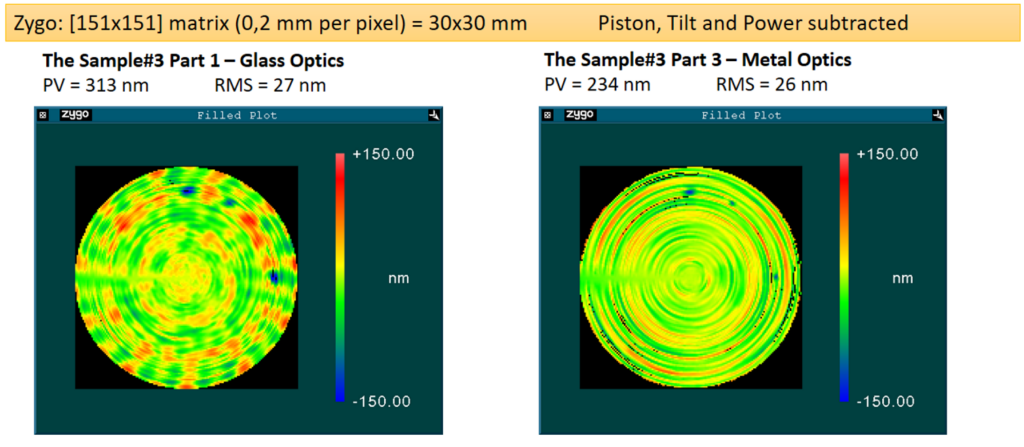
Um die Praktikabilität und Genauigkeit des DaOS-Prinzips für gekrümmte Oberflächen zu demonstrieren, beteiligt sich die Firma Hofbauer regelmäßig an „Round Robin Tests“, die von der Physikalisch-Technischen Bundesanstalt (PTB Braunschweig) angeboten werden [12th HLEM 2022 – High Level Expert Meeting Asphere Metrology]. Hierbei werden Prüflinge zu Verfügung gestellt, die von verschiedenen Labors weltweit unter Einsatz vielfältiger Messmethoden bestimmt werden. Zwei asphärische Linsen (HLEM#3 Part 1 und 3) sind dabei besonders geeignet für die Untersuchung mit dem DaOS-Prinzip, da sie gleiche asphärische Design-Parameter aufweisen bezüglich der Form, aber unterschiedlich hergestellt werden (Part 1 ist eine Glaslinse, die geschliffen und poliert wurde, Part 3 ist eine Metall-Linse, die diamantgedreht wurde). Die Prüflinge haben einen Durchmesser von 30 mm und einen Krümmungsradius im Scheitel von 20,2 mm. Zur besseren Vergleichbarkeit wurden der Oberfläche eine Markerstruktur aufgeprägt, die eine eindeutige Orientierung erlaubt. Die Markerstruktur ist ca. 0,5 mm im Durchmesser und ca. 150 nm tief und optisch nicht sichtbar. Die folgende Übersicht fasst die Messparameter für die beiden Messungen an Prüfling 1und 3 in einer Tabelle zusammen.

Die gesamte Messzeit kann reduziert werden für spezifische Messaufgaben. In unserem Fall wurde mit einer Laborversion ein vollständiger Scan der gesamten Oberfläche ausgeführt und die Positionierung des Messkopfes erfolgte manuell. In einer automatisierten Lösung mit optimierter Prozesssteuerung für industrielle Anwendungen kann die Messdauer signifikant reduziert werden. Einer grobe Abschätzung zufolge kann die gesamte Messdauer einer vergleichbaren Probe auf deutlich unter eine Stunde gebracht werden. In Bild 24 werden zwei zirkulare Scans bei unterschiedlichen Radien für die beiden Proben gegenübergestellt.
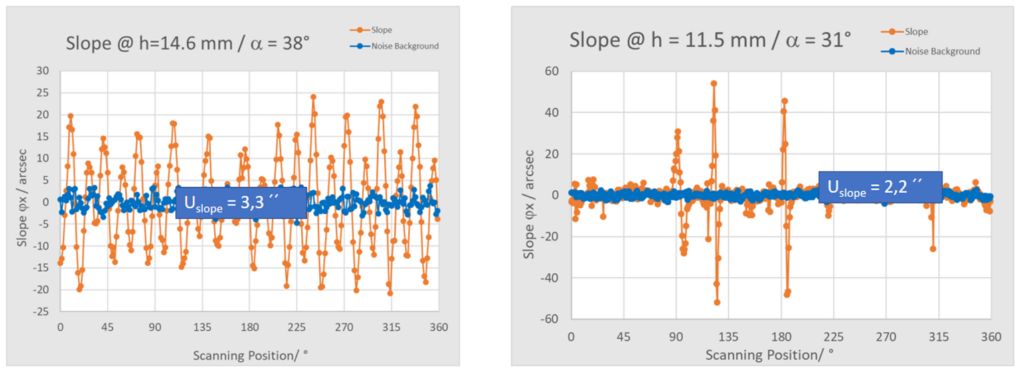
Die linke Seite zeigt den randnahen slope error für die Glas-Probe. Hierbei zeigt sich eine periodische Struktur, die deutlich über dem Streubereich von 3,3“ liegt. Auf der rechten Seite ist im Gegensatz dazu keine periodische Struktur auszumachen. Aber der Radiuswert wurde so gewählt, dass die Marker deutlich sichtbar werden. Abgesehen davon zeigt sich aber keine signifikante Abweichung, welche die natürliche Streuung von 2,2“ übersteigt. Der kleinere Streuuntergrund ergibt sich aus der deutlich stärkeren Reflektion von Metall gegenüber Glas und damit eines verbesserten Signal-Rausch-Verhalten.
Spektrale Analyse der Slope Error Messung
In diesem Kapitel werfen wir einen näheren Blick auf die slope-error-Daten für verschiedene Zonen (d.h. für verschiedene zirkulare Scans bei radialer Position h). Zur Analyse von periodischen Mustern verwenden wir die Fouriertransformation (FFT) der gemittelten und interpolierten Daten, um die Amplituden als Funktion der Winkelfrequenz (1/°) zu bekommen.
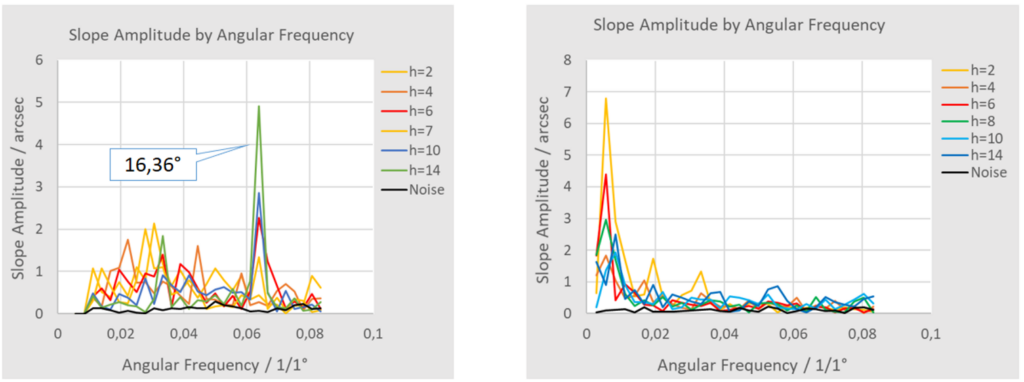
Auf der linken Seite von Bild 25 sehen wir einen dominaten Peak bei einer Winkelfrequenz von 0,061 1/°. Dies entspricht einer Frequenz von f = 22 oder einer Winkelperiode von 16,36°. Die Amplitude steigt mit steigenden Abstand h zur Mitte und dominiert das Spektrum außerhalb h>10 mm. Zusätzlich sind Anteile bei kleineren Frequenzen sichtbar.
Im Gegensatz dazu zeigt die Metall-Optik ein komplett verschiedenes Muster. Hier sind so gut wie keine dominaten höher-frequenten periodischen Strukturen sichtbar.
Wie in der Veröffentlichung von Kukso et al. [12] gezeigt wurde, kann eine spektrale Analyse genutzt werden, um den Produktionsprozess zu qualifizieren. In einer ersten Interpretation der Daten können wir annehmen, dass die Glas-Optik noch Reste des Schleifprozesses zeigt, der die mittelfrequeneten Fehler (MSFE) mit einem Peak bei 16,36°, sichtbar als periodische Struktur, verursacht.
Die Metall-Optik zeigt keinerlei solche periodische Strukturen auf dieser Skala in der zirkularen Richtung auf. Aufgrund des komplett anderen Fertigungsprozesses (Diamantdrehen statt Schleifen) ist dies durchaus verständlich.
Oberflächenprofile und Vergleich mit Interferometrie
Basierend auf den Ergebnissen der slope error Messungen, können wir die Oberflächenprofile rekonstruieren nach den Methoden, die bereits in vorherigen Kapiteln beschrieben wurde. Aufgrund der Tatsache, dass wir nur die sagittalen Winkelwerte für die Rekonstruktion berücksichtigen, bekommen wir keine radialen Modulationen wie Power, Sphärische Aberration oder höhere radiale Terme. Daher sehen wir im folgenden Bild 26 nur die Formabweichungen.
Auf der linken Seite von Bild 26 sehen wir wieder die bereits bekannte „Speichenrad“-Struktur. Zusätzlich ist deutlich die Markerstruktur (blaue Punkte an Rand) zu sehen. Der innere Teil ist dominiert von niederfrequenten Anteilen. Im Gegensatz dazu zeigt die Metall-Optik keine periodischen Strukturen in zirkularer Richtung. Aber die Markerstruktur ist auch hier deutlich sichtbar. Die Marker erscheinen etwas kleiner, da die Schrittgrößen bei der Messung hier um einen Faktor 2 kleiner war und somit die Auflösung deutlich besser. Im linken Bild erscheinen die Marker leicht verschmiert aufgrund der schlechteren Auflösung.
Die ringförmigen Strukturen auf der rechten Seite sind messtechnische Artefakte. Eine spektrale Analyse zeigt kein periodisches Pattern, sondern eine zufällige Verteilung, im Einklang mit unserer vorherigen Aussage, dass in radialer Richtung keine Abweichung gemessen wird. Die Ringstrukturen nehmen zum Rand hin zu und sind Folgen eines Integrations-Artefakts. Im Falle von verrauschten Daten (uslope ~ 2,2‘‘) erzeugt die Integration dominante niederfrequente Muster (1/F Gesetz) in der Höhenintegration. Die Höhe dieser Muster kann aus der Rauschamplitude abgeschätzt werden und beträgt hier in etwa 10-30 nm [11] zum Rand hin, ansteigend mit ansteigender Schrittweite vom inneren Teil der Linse zum äußeren Teil. Dieses Verhalten ist von rein statistischer Natur und erklärt das radiale Muster auf der rechten Seite (Metall-Optik). Das gleiche Verhalten ist auch bei der Glas-Optik sichtbar, wird aber visuell von dem „Speichenrad“-Muster domiert. Bild 27 zeigt einen Vergleich der Profile aus dem DaOS-Prinzip mit einer interferometrischen Messung der Fa. Dioptic, um die Validität des Verfahrens zu bestimmen. Um den Fokus stärker auf die mittelfrequenten Fehler (MSFE) zu legen, wurde in beiden Fällen die ersten 36 Zernike-Ordnungen abgezogen.
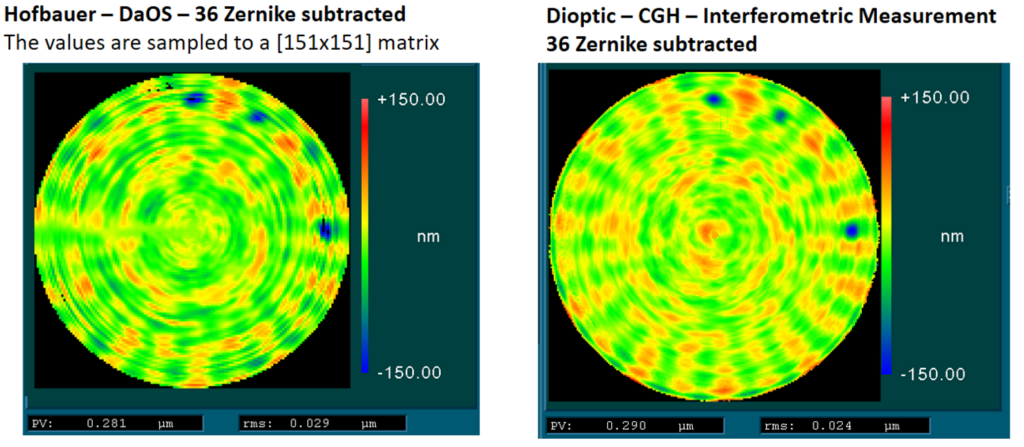
Die periodischen Strukturen (MSFE) sind sehr ähnlich. Die Marker sind deutlich erkennbar, obwohl sie in unserem Fall etwas verschmiert sind. Dies wird durch minimale Abweichungen der exakten Scan-Nullposition für verschiedene Positionen h verursacht. Durch eine automatische Prozesskontrolle der Scans kann dieser Fehler minimiert werden. Im Allgemeinen zeigt sich aber, dass das rekonstruierte Profil aus dem DaOS quantitativ und qualitativ sehr gut mit der interferometrischen Messung übereinstimmt und beweist hiermit die Einsatzfähigkeit zur Bestimmung der mittelfrequenten Fehler einer optischen Oberfläche.
Zusammenfassung und Ausblick
In den vorherigen Kapiteln konnte gezeigt werden, dass wir mithilfe der V-SPOT-Technologie in der Lage sind, die slope errors von optischen Oberflächen mit hoher Genauigkeit zu vermessen. Eine Analyse der Amplituden in der Winkelfrequenz erlaubt die Bestimmung der Unterschiede verschiedener Herstellungsprozesse. Im Bereich der Glas-Optiken sehen wir dominate periodische Strukturen, die auf mittelfrequente Fehler (MSFE) aus dem Schleifprozess hinweisen. Im Gegensatz dazu zeigt die Herstellung von Metall-Optiken auf dieser Skala keine nennenswerten Abweichungen. Die klare Auflösung der Markerstrukturen zeigt, dass der „footprint“ klein genug ist, um diese Strukturen im Sub- Millimeterbereich aufzulösen. Zusätzlich zur Analyse der slope error Messungen zeigt die vollständige Rekonstruktion der Oberfläche eine dominante „Speichenrad“-Struktur für die Glas-Optik. Im Gegensatz dazu zeigt die Metall-Optik ein glattes Profil ohne diese periodischen Strukturen entlang der Scan-Richtung.
Ein Vergleich mit interferometrischen Messungen beweist die Präzision und Auflösung des DaOS-Aufbaus.
In der folgenden Tabelle 5 werden die wesentlichen Aspekte des Labor-Aufbaus zusammengefasst und Abschätzungen für eine zukünftige kommerzielle Version gegeben.

Ausblick
Obwohl das Profil akkurat aus den zirkularen Scans rekonstruiert werden kann, werden wir den Aufbau so erweitern, dass auch in radialer Richtung exakte Rekonstruktionen möglich sind, und damit die Design-Parameter der Asphäre bestimmt werden können. Aufgrund der kleinen Krümmungsradien (R0 im Zentimeter-Bereich) und daraus resultierenden großen Randwinkel für kleine Optiken, müssen wir die Einfallswinkel a exakt bestimmen und mit hoher Präzision messen. Dann können wir mit einem Satz von sagittalen (Zirkular) und meridionalen (Radial) Winkelwerten eine komplette Oberfläche inklusive der Form der Linse bestimmen. Damit ließe sich jede beliebige Asphäre bestimmen, ohne zusätzliche Kosten für CGH, wie sie in der Interferometrie üblich sind.
In einem gemeinsamen Projekt mit Start in 2022 mit der Hochschule Deggendorf wird ein neuer Aufbau entworfen und getestet, um die entsprechende Mathematik zur Analyse der Daten zu erarbeiten, eine prozessuale Steuerung zu entwerfen und zu testen und anhand gezielter Messungen die Grenzen des Verfahrens zu bestimmen und auszuweiten.
Literaturverzeichnis
[1] E. Debler, K. Zander: „Ebenheitsmessung an optischen Planflächen mit Autokollimationsfernrohr und Pentagonprisma“, PTB Mitteilungen Forschen + Prüfen, 89. Jahrgang (1997).
[2] I. Weingärtner, C. Elster: „System of four distance sensors for high- accuracy measurement of topography”.Precision Engineering, 28, (S.164-170) (2004)
[3] H. Lammert, T. Noll, T. Schlegel, F. Siewert, T. Zeschke: „Details XUV-Optik – Neue unkonventionelleBestimmung ihrer Flächenformen bei BESSY mit der NOM.“ DgaO 105. Tagung(2004)
[4] E. Hofbauer, R. Rascher, M. Schilke, F. Friedke, J.-P. Richters: “Deflectometric acquisition of large optical surfaces “DaOS” using a new physical measurement principle: vignetting field stop procedure, Proc of SPIE Vol. 10009, 100090A (2016)
[5] E. Hofbauer, M. Lenz: „Vignettierung als physikalisches Messprinzip.“ Technisches Messen 75, 3 (2008)
[6] S. K. Barber, et al.: Developmental long-trace profiler using optimally aligned mirror-based pentaprism; Optical Engineering 50 (5), 053601 (May 2011).
[7] E. Hofbauer: „Optisches Verfahren zur zweidimensionalen Messung von Winkeln und Winkeländerungen bei großen Messabständen.“ Dissertation (2007)
[8] Valeriy V. Yashchuk, Optimal measurement strategies for effective suppression of drift errors; Citation: Review of Scientific Instruments 80, 115101 (2009); doi: 10.1063/1.3249559; Published by the American Institute of Physics
[9] Dr.-Ing. J. Kanta: “Einsatzmöglichkeiten von Richtungs- und Fluchtungsprüfgeräten für die Formprüfung“, Feingerätetechnik 19. Jg. Heft 12/1970
[10] Prof. Dr.-Ing. habil W. Lotze: Bemerkung zum Aufsatz Kanta: >Einsatzmöglichkeiten von Richtungs- und Fluchtungsprüfgeräten für die Formprüfung<, Feingerätetechnik 20.Jg. Heft 4/1971
[11] E. Hofbauer, R. Rascher, F. Friedke, R. Kometer: “Resolution, measurement errors and uncertainties on deflectometric acquisition of large optical surfaces ‘DaOS’“, Proc. of SPIE 10326 1032603-12, Sept. 2019
[12] O. Kukso, R. Rascher, R. Börret, M. Pohl, „On the metrology of MSF errors after grinding,“ Proc.
of SPIE 10742, Optical Manufacturing and Testing XII, 107420X (14 September 2018)
[13] R. Kometer, E. Hofbauer, „Fast and reliable in-situ measurements of large and complex surfaces using a novel deflectometric device “, Proc. SPIE 10829, August 2018
[14] R. Kometer, E. Hofbauer, „Knowing the limits: surface deviation in the midspatial frequency range by deflectometric measurements,“ Proc. SPIE 11853, June 2021
* Dr.-Ing. Engelbert Hofbauer, Dr.-Rer.nat. Ronald Kometer
HOFBAUER OPTIK Mess- & Prüftechnik, München